网络计划技术在新产品生产定型技术准备及试制中的应用
出处:按学科分类—经济 企业管理出版社《现代企业内部会计实用手册》第1118页(2792字)
一、问题的提出
在许多研制性开发性工程中,由于牵连的因素较多,又要受到一些随机因素的影响,而且还要受到人们对研制对象认识程度的限制,会使每项工序的作业时间不能事先非常精确地给定。往往只能根据不同的条件做出粗略地估计,而不同的估计所得的数值显然是不同的。既然工序时间是一种估计时间,据此所求提的网络时间参数的计算结果也就存在着某些不确定的因素。因此,就很有必要研究由于这些不确定因素所引起生产任务是否能够按期完成的问题,以便于对整个计划是否能按期完成给予概率评价,并对计划的执行做出预测。
二、某产品生产定型技术准备及试制计划网络图
某厂准备生产一种新产品,已经设计定型,现要求在本年度内完成生产定型,适应下一年度的外贸任务的需要。为了保证总定型进度,工期至多为44周,而为了尽早进行现场试验,希望在42周内完成。
根据产品设计和生产条件,进行了任务分解,并确定各工序关系如表11。对各工序的作业时间,凭经验和依据过去的试验研究结果估计出三种可能时间列于表11的最后一列。其中,a表示乐观估计时间,m表示最可能的估计时间,b表示悲观估计时间。
表1

按表11所示各工序的逻辑关系,绘制此计划项目的网络图为图11所示。图上所示各工序的完成时间系按“三点估计”公式

计算的平均工序时间。
在图11中,对外协件只描述了工序关系,其进度以确保计划实施为前提。
对上述网络图进行网络时间参数的计算(计算过程略)可以得出此网络计划的两条关键路线,在图10中用黑线表示。

图10
CP1:①→②→④→⑦→⑾→⒀→⒁→⒂→⒃→⒄→⒅
CP2:①→②→④→⑥→⑧→⒁→⒂→⒃→⒄→⒅
而其工期为23天。
三、关键路线和任务按期完成的概率分析
由于网络时间参数计算中所依据的工序时间是种估计的平均时间,为反映这种估计时间代表性的大小,也就是反映各工序时间代表性的大小,也就是反映各工序时间概率分布的离散程度,而由方差公式。
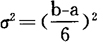
得其均方差为

σ的数值愈大,表示工序时间概率分布的离散程度愈大,平均估计时间的代表性愈小;而σ的数值愈小,表示工序时间概率分布的离散程度愈小,平均估计时间的代表性就愈大。
由表11所示各工序的估计时间,可计算图11各工序的均方差,结果列于表12。
表2

在图11中所示网络图中,存在着两条关键路线,那么,这两条关键路线,哪一条更为关键呢?显然,对更关键的路线,在计划实施过程中,应该特别予以关注。为此,可计算两条关键路线的均方差,其均方差最大的路线便是最关键路线。其计算过程如下:


由于σcp<σcp2,所以CP2为最关键路线。
因为编制的网络计划要受到一些不确定因素的影响,所以,就有必要来研究这些不确定因素是否影响计划按期完成,这就是任务是否能按期完成的概率分析。
为了使用方便,用系数λ来表达网络计划编制后在规定日期实现的难易程度,称为难易系数(或称为概率系数)。难易系数λ可用下式求得

其中,T为任务规定的总工期,TE为预计总工期,σcp为关键路线上的均方差。根据求得的概率系数λ,便可由标准正态分布表中查得任务按期完成的概率P(λ)。一般,当P(λ)接近于0时,在指定日期完成的困难很大,未留有余地;当P(λ)接近1时,表明易于在指定日期完成,留有较大的余地;当0.30≤P(λ)≤0.70时,在指定日期完成是可能的,计划订得比较合理。
在本例中,经计算的预计总工期为43周,而根据定型任务的要求,工期至多为44周,以最关键路线CP2的均方差来进行计算,可有

查正态分布表,可知P(λ)=0.802,即说明按期完成计划的可能性为80.2%。显然,在44周完成是较容易的。
而若要求在42周内完成,可计算出

查正态分布表知P(λ)=0.198。这表明计划在42周完成的可能性只有19.8%,因此,是很难完成的。
为缩短工期,加快进度,保证能在42周完成,可对有些工序采取平行作业或交叉作业。如把试制批的制造与交验两道工序⒁12→O⒂3→P⒃变成如下关系:

图2
对改进后的网络图进行计算,可知计算工期为41.5周。同样对关键路线进行分析,得σcp2=1.05,于是有

查得P(λ)0.684,说明有68.4%的可能在42周内完工。