计数标准型二次抽样方案

出处：按学科分类—经济 中山大学出版社《质量工作者手册》第220页（1085字）

二次抽样的抽检工作量平均来说比一次抽样要小些，为了节省抽检量和费用，应采用二次抽样方案，皮奇(Paul Peach)编制了计数标准型二次抽样方案表(表9－1)，此表是基于α=β=0．05的设定编制的，其使用程序如下：

(1)产销双方商定P₀和P₁。

(2)计算P₁／P₀，得出计算值。

(3)在抽检表9－1的P₁／P₀列找到最接近且大于计算值的那一行。

表9－1

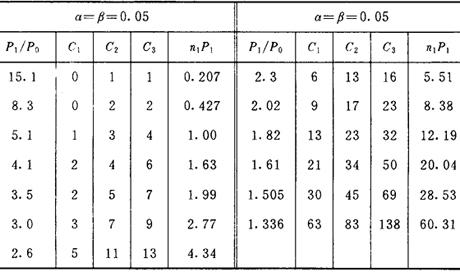
(4)读取这一行中的C₁，C₂，C₃，和n₁P₁值。

(5)将n₁P₁值除以P₁，得出n₁(弃去小数)。

(6)得出计数标准型二次抽样方案如下：第一样本大小n₁，第一合格判定数A₁=C₁，第一不合格判定数R₁=C₂；第二样本大小n₂=n₁，第二合格判定数A₂=C₃，第二不合格判定数R₂=C₃+1。

(7)按此方案的抽检程序是：先从交验批抽取第一样本n₁，经检验发现其中有d₁个不合格(品)，如d₁≤C₁，判批合格；如d₁≥C₂，判批不合格；如C₁＜d₁＜C₂，则再抽取一个大小为n₂=n₁的第二样本，发现其中有d₂个不合格(品)，如d₁+d₂≤C₃，则判批合格；如d₁+d₂＞C₃，则判批不合格。

例：规定α=β=0．05，P₀=0．5(%)，P₁=1．5(%)，求满足这些规定的二次抽样方案。

(1)计算P₁／P₀=1．5／0．5=3；

(2)在表9－1中找到P₁／P₀=3所在的列；

(3)在P₁／P₀=3的列中读取C₁=3，C₂=7，C₃=9，n₁P₁=2．77；

(4)n₁=n₁P₁／P₁=2．77／0．015=184；

(5)n₂=n₁=184。

故所求的抽样方案是：n₁=n₂=184；C₁=3，C₂=7，C₃=9。