计算投资收益率
出处:按学科分类—经济 上海人民出版社《金融工具手册》第24页(23277字)
在建立投资目标、决定策略、配置资产和执行交易后,下一个任务是评估投资组合的价值,并启动业绩测量程序。无论投资者是自己制定投资决策还是将这项任务授权给顾问,所有各方都对计算和权衡结果感兴趣。业绩测量程序的第一个阶段是计算收益,它是在投资者冒险投资的资本上赚取的收入和利润。
假设投资者将$100投资于一家基金,基金随后升值,从而投资者收回了$130。该投资的收益是多少?投资者赚取了$30。将这个美元收益除以其投资的$100,并将小数结果0.3乘以100将给出用百分比表达的收益率,即30%。
收益率是用百分比表示的在一段时期内从投资获取的收益。收益率是将收益金额与冒险投资的金额联系起来的比率。我们将30%的收益率解释为在这段时期内相当于$100的原始投资额的将近1/3的收益。
尽管计算和解释收益率似乎不需要任何特殊的投资知识,但有数个复杂之处使我们值得进一步考察这个主题:
□ 在收益率的计算中选择恰当的输入信息
□ 处理客户在投资账户中的额外供款和提款
□ 调整收益率以反映这些供款和提款的发生时间
□ 区分投资经理产生的收益率和投资者实际获得的收益率
□ 计算跨多个评估期的收益率
□ 计算定期收益率的平均值
这些是我们将在本章中讨论的问题。其中,我们总结了已发展为投资行业标准的投资组合收益率计算和报告方法。通过独立账户或混合账户进行投资、并利用各种策略和资产类别的个人和机构投资者,都采用本章介绍的方法计算其投资组合赚取的收益率。无论你是监测你的私人经纪账户业绩的个人投资者、为许多个人提供建议的理财规划师、共同基金经理,还是监管数十位专业投资经理的养老金计划发起人,这里介绍的工具都是相关的。在解释本章介绍的各种概念的例子中,我们采用了电子制表软件的格式,以使读者更容易复制这些计算。
单期收益率
为什么我们在可以简单地用所获得的绝对美元金额判断业绩的同时,要通过计算收益率描述一项投资的业绩?毕竟,没有什么是比银行中的现金更佳的判断标准了!收益率成为总结投资业绩的优选统计值有数个原因:
□ 收益率将大量信息集中于单个统计值中。有关期初和期末市场价值、赚取的收入、现金供款和提款,以及投资组合中所持全部证券的交易的数据都被压缩在了一个数字中。
□ 这个数字——收益率——是一个比率。投资者分析比例的速度要比分析绝对数字快。例如,假如一位投资者被告知她赚取了8%的收益率,她可以立即开始判断她是否对这个结果感到满意,而不需要先仔细查看估值和交易报表。
□ 即使是在基础数字不可比较的情况下,收益率也是可比的。即使多个投资组合具有不同的基础货币或规模,投资者也可以比较它们的收益率。例如,假如一位投资者投资$100并赚取了$10,那么她与一位投资$100万并最终拥有$110万的投资者赚取了相同的收益率。
□ 不同时期计算的收益率是可比的;也就是说,投资者可以比较今年与去年的收益率。
□ 收益率的解释具有直观性。收益率是在我们的测量期内比较期初投资价值与期末价值的数值。投资者可以在给定投资额的情况下,利用报告的收益率确定他在期末将拥有的金额。
MVE=MVB×(1+小数收益率)
其中,
MVE=期末市场价值
MVB=期初市场价值
例如,假如我们以40%的收益率投资$100,那么将在期末拥有$140:$100×(1.40)=$140。在做乘法之前将1与小数收益率相加将给出一个等于期初价值加这段时期内的收益/损失的结果。乘以0.4的收益率将给出这段时期内的收益/损失($40)。
让我们更仔细地考察收益率的计算。在我们的引言例子中,我们在$100的投资上赚取了$30的收益。利用以下公式,我们通过将收益除以投资额,得出了30%的收益率:

假设我们不是在单个时期内投资并收回资金的,而是在期初持有价值$100的投资,并在期末其价值为$130时继续持有该投资。将第一个比率乘以100使小数形式的比例转换成了百分比收益;在我们的例子中为30%(0.3×100=30%)。
无论投资者是在一个时期内购买并清算投资还是紧接着上一个时期继续持有该投资的,我们都可以计算相同的收益率。当我们测量我们购买并跨时期持有的投资的收益率时,我们将期初市场价值当作在这段时期内新作的投资,并将期末市场价值当作从在期末出售该投资获得的收入。
至此为止,我们利用了两种形式的收益率计算。利用哪种并不重要。这两个方法是等价的。
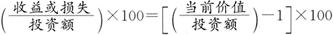
我们可以通过从第一种计算形式推导出第二种,说明两个形式是相同的。

利用第一种形式,收益率计算中的分子为未实现的收益或损失:期初市场价值与期末市场价值的差额。假如投资期间存在赚取的收入,那么我们将之也加入到分子中,以使分子更恰当地变为市场价值加应计收入。在两种形式的计算中,分母都是投资额。我们选择的分母数字代表了该时期内的涉险资金。在第一个测量期,投资额等于最初投资于投资组合的金额。在随后的测量期中,它等于前一个时期的期末市场价值。以下电子数据表提供了我们在12月末投资$100,并且该投资在1月份上升至$110、并在2月份上升至$120的收益率计算。

注意,即使我们在1月份和2月份都赚取了同样$10的收益,但1月份的百分比收益率(10/100=10.00%)高于2月份的收益率(10/110=9.09%)。2月份的收益率更低的原因在于:2月份的涉险资金不仅等于$100的原始投资额,而且还包括1月份赚取的$10收益。由于冒险投资的资金更多,因此相同的美元收益导致了更低的投资收益率。
通过利用投资的市场价值计算收益率,即使我们未在期末出售投资以真正实现收益,也仍会确认该投资收益。为了计算包含未实现收益的收益率,我们在每个测量期末评估投资组合的价值。这些日期是定期的估值日。在两个估值日期间计算的收益率叫做单期收益率、持有期收益率或定期收益率。单期收益率的周期与投资组合估值的频率相关。例如,我们可以在每晚市场收盘时估计共同基金的价值以每日计算其单期收益率,但仅每月计算机构独立账户的单期收益率,并每季计算房地产合伙公司股份的单期收益率,因为此类资产的估值没有如此频繁。估值的执行频率至少与参与者可以将资金注入或转移出混合基金的频率相同。
单期收益率的成分
当投资账户中没有资金进出交易并且投资期内没有赚取的收入时,我们在计算单期收益率时只需要简单地将期末市场价值除以期初市场价值。投资组合的市场价值总额是通过将基金中所有基础投资的价值相加起来得到的。假如我们计算的是在我们的混合投资组合(如共同基金)份额上赚取的收益率,那么市场价值等于我们持有的份额总数乘以估值日的每份单位价值。单位价值是通过将组成基金的个体证券市场价值总和除以流通份额总数计算的。投资组合的持有仓位是在交易日确定的。在交易日会计法中,我们在投资经理同意购买或出售证券的当日将这些证券包含在投资组合的估值中,而不是等到与经纪商清算交易的那一日。
每种证券的市场价值是假如投资被在估值日出售,我们预期将获得的金额。它是利用我们观察到的市场价格和汇率(在适用时)计算的。确定市场价值对于诸如在交易所交易的股票等工具十分简单,但我们还需要估计其他类型的投资的最新价值。例如,不经常交易的债券是参考在当日发生交易的类似债券的价格逐日盯市的。尽管由于流动性等原因,如果我们真正出售该投资工具,那么将有可能不能实现我们在估值中所用到的市场收盘价,但这个方法避免了将对交易产生的影响的主观估计引入到收益率计算中。假如基金中持有现金,那么它也被包含在基金的估值中。
个体证券的市场价值包含对投资赚取的收入或应计收入的测量。应计收入是已经赚取、但尚未收到的收入。例如,假如一位投资者在两个息票日期间出售债券,那么该投资者也将自上一个息票支付日起累计的利息出售给了债券的买方。由于假如证券是在估值日出售的,其出售的利息也将成为收入的一部分,因此我们也将之包含在市场价值的计算中。同时反映市场价值的变化和在投资期内赚取的收入的收益率叫做总收益率。我们也用同样的方式按基金的应收和应付款项调整投资组合的市场价值总额。例如,我们从市场价值总额中减去应支付给投资经理的应付管理费。
尽管详细列举基金可以投资的每种证券的估值细节在本章范围之外,但我们利用由市场报价驱动、并且基于交易日和应计收入的估值原理判断投资组合中每种证券的价值,然后在投资组合水平计算这些价值的总和,并得出单期收益率的计算公式:

我们有必要指出我们在收益率计算中未明确包含的因素。在第一个时期的收益率计算以后,我们不在业绩测量中考虑投资成本(以摊还成本估值的证券除外)。在随后的每个时期中,上一个时期的期末市场价值被用作下一个时期的期初市场价值。这种做法的理由在于:我们假设投资周期在每个估值期都重新开始,在下一个时期投资(或涉险)的金额是当前市场价值,而不是原始成本。
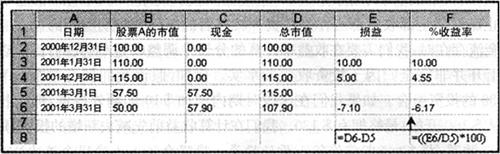
收益率计算未涉及在投资期内的证券出售中已实现的收益。事实上,投资组合的期初和期末市场价值同时包含投资期内的投资组合交易所产生的未实现和已实现资本增值。让我们考虑具有以下系列活动的投资组合:
2000年12月31日
□ 持有100股每股$1的股票A=$100MVB
2001年1月31日
□ 股票A的估值为$110,1月份的收益率为(10/100=10%)
2001年2月28日
□ 股票A的估值为$115,2月份的收益率为(5/110=4.55%)
2001年3月1日
□ 以每股$1.15的价格出售50股股票A,净获得$57.50
□ 在股票出售中实现的收益为$7.50($57.50-$50=$7.50)
□ 用股票抛售收入以每股$5.75的价格购买10股股票B
2001年3月31日
□ 股票A的估值为(50股×$1=$50)
□ 股票B的估值为(10股×$5=$50)
□ 投资组合的总价值为$100,3月份的损失为(-15/115=-13.04%)
下列电子数据表显示了我们在3月份的收益率计算中未明确利用$7.50的已实现收益。

出售股票A实现的收益被用以购买股票B,然后,我们在3月末调整股票B的市值。我们明确计算了该时期内的未实现市场价值变化(-15.00),这个市场价值变化隐含了在该段时期内出售证券的所有已实现收益/损失。
投资经理也有可能不通过购买另一种证券以对股票抛售收入进行再投资。在这种情形下,我们仍不在收益率计算中明确包含已实现收益。相反,我们在基金的市场价值总额中包含出售股票所获取的现金。以下电子数据表说明了我们无需知道投资组合在估值期内的交易即可以计算投资组合的业绩。
投资组合在估值期内的交易并不影响基金层次的总收益率计算,因为它们对业绩具有同等但相反的影响--购买一种证券即意味着出售另一种(现金)。这对在估值期内获取的收入也同样如此。在一种证券上获得的收入是从该证券的流出,但却是一种现金流入。为了计算在无额外供款和提款情形下的投资组合业绩,我们仅需要计算基金中的所有证券在持有期内的期初和期末市场价值以及现金余额。
投资收益率(ROI)
至此为止,我们已在我们可将所持工具的市场价值用作下一个时期初的投资的情况下考察了单期收益率的计算。个人和机构投资者还定期在投资账户中增加额外投资(或供款)和从投资账户中提款。这些基金的净供款不被包含在投资收益率的成分中;它们代表的是涉险资本的增加,而不是投资的资本利得。由于这个原因,当基金获取新资金时,我们不能通过简单地观察市场价值的变化来测量业绩。
这些进出基金的资产转移有时被称为现金流。现金流是适用于不同交易类型的一般术语。对于待遇确定型养老金计划,现金流包含公司定期为计划提供的资金和为向退休人员支付养老金所进行的提款。对共同基金而言,现金流包含基金份额的购买或清算,以及基金之间的份额转换。图3.1显示了投资者、投资经理和投资组合的一般交易关系。

图3.1 现金流
现金流的价值是存入或提取的资金的金额。大于零的现金流为流入基金的资金。小于零的现金流为流出基金的资金。有时,供款是以证券、而不是以现金的形式完成的。例如,这会在投资组合被转移给新的投资经理时发生。这些“实物”供款的货币价值是用在供款时被转移的资产的当前价值测量的。在这些情形中,我们必须利用当前市场价值、而不是原始成本。假如我们利用原始成本,那么在供款后的第一个时期的收益率计算将会把至此为止赚取的全部收益都当作是在资产转移后的第一个时期赚取的。
当现金流存在时,我们需要在收益率计算的分子中调整收益/损失的计算,以考虑到市场价值的上升并非完全归因于投资收益的事实。例如,假设我们拥有一个MVB为100、MVE为130的投资组合。如果我们在这段时期内增加$10的额外投资,那么收益将是多少?我们从$100开始,最终拥有$130。我们在计算收益前先减去新增的投资额:
收益/损失=(当前价值-原始投资-净现金流入+净现金流出)
在这种情形下,收益为$20(130-100-10+0)。这段时期内的$20的收益/损失结合了两个金额——在原始的$100上获取的收益和在$10的新增投资额上赚取的收益。假如我们没有净现金流入,而是由于在这段时期内从投资组合中提取了资金而发生了净现金流出,那么第二个成分将是在提取资金前赚取的收益。
当现金流存在时,我们除了修正分子外,还需要修正收益率计算的分母,以考虑到测量期内新增或提取的资本。我们可以修正收益率计算以考虑到新增投资或提款。由此得出的结果为投资收益率(return on investment,ROI)公式。投资收益率是在根据供款和提款做出调整后,用投资额的百分比表达的投资收益或损失。

其中,NIF为净现金流入,NOF为净现金流出。以下电子数据表显示了投资收益率的计算。

分子中的第一个表达式(EMV+NOF)代替了在投资收益率的计算中利用的EMV。我们对期末市场价值做了投资组合提款的调整。注意,这提高了分子和由此得出的收益率。提款被当作是有利于业绩的。在第二个表达式中,我们减除了投资额以计算收益。现金流入被当作是投资,这减少了收益。供款被当作是对业绩的损耗。投资总额(BMV+NIF)是投资收益率的分母。通过在BMV上添加供款额,我们降低了收益率,因为我们将相同的收益除以了一个更大的数字。
当BMV=100、EMV=130并且NIF=10时,18.18%是解释该情形的公平收益率吗?回答是,这要视具体情况而定。注意,这里的隐含假设是NIF在整个时期内都可被用于投资或涉及风险。假如这笔新增的现金流入是在期初注入基金的,那么投资者在整个时期内都不能利用这笔资金。投资者将期望获得比在让其保留资金、并仅在期末将之投资于基金的情形下更高的基金收益率以补偿这点。因此,收益率应考虑到新增现金流的发生时间。假如投资是在测量期内的某个时候作出的,那么投资者确实可在部分时期内利用这笔资本。例如,假如测量期为1个月,并且$10的供款在当月的月中发生,那么基金在前半个月拥有$100的投资资本,并在后半个月拥有$110。$20的收益是在更低的投资余额上赚取的;因此,该账户的收益率应高于18.18%。
尽管投资收益率根据投资组合的供款和提款作出了调整,但它未根据这些现金流的发生时间作出调整。由于供款可在整个时期内利用的假设,无论现金流在测量期内的何时发生,投资收益率都会给出相同的收益率。投资收益率作为投资业绩测度的另一个缺陷是:它未根据持有期的长度作出任何调整。无论收益是在1天、1年或10年内赚取的,投资收益率的计算都将给出相同的结果。由于这些原因,我们需要一个同时反映现金流的发生时间和资产涉险期长度的收益率测度。这两个调整都从与金钱的时间价值相关的概念推导而来,我们将在下面讨论金钱的时间价值。
金钱的时间价值
我们可以将收益率与在固定收益投资的未来价值计算中利用的利率等同起来。然而,与收益率不同,利率是事先已知的,因此我们可以在期初预测未来价值。投资的未来价值等于现时价值加在该时期内赚取的利息和其他收益。
FV=PV×(1+R)N
其中,
FV=期末价值
PV=投资的当前价值
R=每个时期赚取的收益率
N=估值期的时期数
在收益率的计算中,R是未知的。我们利用我们观察到的期初和期末市场价值计算这个收益率R。为了推导未来价值的等价变量,即投资在单个时期内的MVE,我们将MVB乘以1加利率。
期末市场价值=期初市场价值×(1+利率)
期末与期初市场价值的差额为投资期内赚取的收益。复合是对收益进行再投资,以在今后时期内赚取更多的收益。在单利的情形下,投资收益未被加以再投资,从而未在接下来的时期内复合利息。例如,假如我们以5%/月的利率对MVB=1000进行4个月的投资,我们计算得出期末价值为1200。
期末市场价值=期初市场价值×[1+(百分比利率/100)×投资的时期数]
=1000×[1+(5%/100)×4]=1200
假如投资者在每个时期末提取其所赚取的收益,那么我们将利用单利进行计算。在这个例子中,四个月内的总收益为$200。将之除以$1000的投资额将给出四个月期的20%的收益率。这等于每月的定期美元收益乘以4。
假如投资者将收益保留在投资工具中或对之加以再投资,那么它们将会累积,并在每下一个时期的收益计算中提高起始余额。例如,假设我们每年复合利息,以7%的利率对$100进行10年的投资将给出$196.72的期末价值。
不幸的是,再投资假设并非对所有投资者都是现实的。例如,任何投资于免税工具(如合格的退休金账户)以外的产品的应纳税投资者都必须对其所赚取的收益纳税。税收降低了可在下一时期内用于再投资的收益。由于这个事实,业绩测量的一个趋势是将税收包含在收益率计算中。

再投资假设十分重要,因为投资的效力在于复合利息,即在先前时期内赚取的利息之上的利息。在赚取7%的年收益率的10年期投资中,利滚利成分占终期价值的14%。在每年7%的30年期投资中,利滚利成分将接近期末价值的60%。
当投资者在每个时期结束时提取利息收益时,单利计算是这种情形的一个更佳测度。假如收益可用来赚取更多收益,那么复利是更佳的测度。我们在所有的投资应用中都假设复利。对利率而言,我们通常假设利息在随后的时期内以相同的利率被加以再投资。收益率计算与利率计算的差别在于:在收益率计算中,尽管我们也假设收益被加以再投资,但我们认识到定期收益率在不同的时期内会上下波动。
尽管我们理解在持有期内赚取更高的收益率将增加期末投资价值,但复合的频率也会影响期末价值。正如以下电子数据表显示的那样,假如收益的复合更为频繁,那么具有相同收益率的投资将具有更高价值。

利率通常是用年利率报价的。我们可以调整年利率报价,以考虑到更频繁的复合:

其中,
r=定期利率
m=每个时期支付利息或复合利息的次数
例如,假如$100的投资在6个月内产生3%的收益率(即MVB=100并且MVE=47 103),那么在假设每半年复合一次利息并对利息加以再投资的情况下,1年末的价值将为$106.09

将时间考虑在内的收益率
基于金钱具有时间价值的事实,让我们回到我们前面考虑过的一个问题:当基金的MVB为$100、我们在投资期内新增$10的投资、并且MVE为$130时,基金的恰当持有期收益率是多少?
无论投资是在投资期内的何时作出的,美元收益都为$20($130-$100-$10)。这段时期内的收益率取决于新增投资的加入时间。收益率可以低至18.18%,或高达20%。假如这笔$10是在期初投资的,那么所用资本等于$100的原始投资加$10的新增投资。

假设新增投资恰好是在投资期末发生的,那么投资期内所用的资本仅为$100,因此收益率为20%。

由于美元收益相同,因此随着供款时间越来越接近期末,我们应赋予总体投资更高的收益率。假如投资是在期末作出的,那么新增的供款将不被包含在分母中。相同的分子除以一个更小的分母将产生更高的收益率。当供款是在期末进行的时,这个更高的收益率是合理的,因为投资期内的涉险资本较低,但我们却赚取了相同的美元收益。
这个例子显示:为了精确地计算收益率,跟踪在投资账户中供款和提款的时间十分重要。我们总是根据投资期内的新增供款或提款调整分子。根据现金流的发生时间,我们或者将全部供款额包含在分母中、或者不将供款额包含在分母中,或仅将部分供款额包含在分母中。当我们根据供款或提款调整收益率计算的分母时,我们称分母为平均所用资本或平均投资余额。
投资业绩:资金加权收益率
在本节中,我们将需要在计算投资者赚取的收益率时同时认识到投资者和投资经理的决策的影响,但在计算归因于投资经理的收益率时却需要分离投资者决策的影响。美元加权收益率或资金加权收益率(money weighted return,MWR)是同时包含这两种决策的影响的投资组合业绩。
投资者的决策时机
除了金钱的时间价值外,投资者供款和提款的市场时机将影响其所实现的收益率。资本市场为我们提供了大于零的长期收益率,但定期收益率却具有波动性。市场时机是将投资者作出投资的时间与市场周期联系起来的术语——即投资者是否低买高卖。
例如,假设我们通过共同基金——第二十一章讨论的一种投资工具——进行投资,基金在某个月份内的每股净资产值(NAV)在10.00和12.00之间变化,并且没有现金分配。

该基金公布的月收益率将为(11/10=10%)。以下电子数据表显示了当月各种持有期收益率的计算。
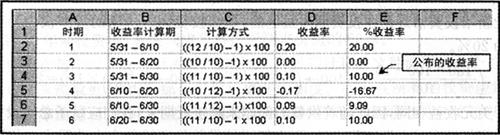
拥有完全远见或运气的投资者在5月31日投资,并在6月10日提款,赚取了20%的收益率。时机选择能力较差的投资者在6月10日的最高点买入,并在6月20日的底部卖出,拥有-16.67%的收益率。这个36.67%的利差代表了因现金流的时机选择不同而导致的收益率差额。投资业绩测量的要点在于,这些现金流是由投资者、而不是由投资经理控制的。投资经理的行动对这个收益率差额没有任何影响;投资经理会根据指令运用资金。
混合基金拥有多个投资者。一些投资者采用买入一持有策略,一些投资者来回交易进出基金,另一些投资者则有定期购买或出售新份额的计划。当市场上升、下跌并回升时,根据不同的现金流和收益率之波动率,不同投资者赚取的收益率可能会有很大差异。当然,本例中的收益率具有人为的波动性。这里说明的要点是:投资者所实现的实际收益率将根据其自身的投资时机决策发生变化。
在上一个例子中,基金公布的投资期收益率为10%,它是从月初测量至月末的。尽管不同的投资者实现了不同的收益率,但共同基金的投资经理对这些时机决策没有任何控制权;因此10%精确地代表了其业绩。它是我们在将其业绩与同行平均业绩或基准指标的业绩进行比较时应采用的恰当收益率。
投资经理的决策时机
我们在计算收益率时,还可以考虑由投资经理负责做出的决策的时机选择。让我们考虑两位都在月初以$100的相同投资组合开始的投资经理。两位经理都收到了$10的客户供款。其策略的不同之处仅在于:经理1试图用本例中所示的方式选择市场时机。假设市场当月下跌了10%。经理1以现金形式保留供款。以下电子数据表显示了经理1的收益率为-9.05%。
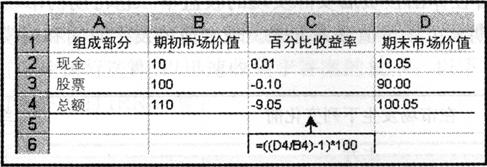
下列电子数据表显示了经理2在月初将供款投资于股票,并实现了-10.00%的收益率。

尽管收益率都为负数,但由于经理1做出的在当月以收益率相对较高的现金形式保留供款的有利决策,其赚取了比经理2高出95个基点[-9.05%-(-10%)]的附加值收益。
将投资者和投资经理的时机决策分离开来
通常,投资经理和投资者不是同一人。前数个小节说明了一个业绩测量问题:我们必须分离投资者和投资经理所做的决策.以恰当地计算分别反映其责任的收益率。
测量投资者所实现的收益率的理想业绩统计值将包含以下两者的影响:
□ 投资者决定将资金投入投资组合的时机
□ 投资经理在投资组合中配置资产和选择证券的决策
第一个影响可纯粹归因于投资者所做的决策。第二个影响也可被认为是归因于投资者的,因为他做出了雇用投资经理的决策。投资者所实现的实际收益率受到这两者之组合的影响。测量投资经理所产生的收益率的理想统计值中和了时机选择的影响,因为他(通常)对外部现金流的发生时间没有控制权。由于这种分离投资者的决策时机的需要,我们需要两个不同的收益率测度。
当我们需要测量投资者所实现的业绩时,我们利用资金加权收益率(MWR)。MWR是反映在测量期内赚取了多少收益的业绩统计值。这个金额受到在投资组合中供款或提款的决策时机以及投资组合经理的决策的影响。MWR与用以测量投资经理业绩的业绩统计值——时间加权收益率(time weighted return,TWR)——形成了对比,本章后面将讨论后一个测度。正如我们将看到的那样,即使我们仅对评估投资经理的业绩感兴趣,MWR也十分重要,因为我们在TWR的估计中有时要用到MWR。
MWR是投资者在作出投资后实际实现的收益率。它将期初市场价值和投资组合中的新增现金流入与期末市场价值联系起来。现金流的发生时间和规模对期末市场价值具有影响:

为了精确地反映这些交易,MWR不仅考虑了现金流的金额,而且还考虑了现金流的发生时机。投资组合的不同投资者将投资不同的金额,并在不同日期进行投资。由于现金流的发生时机和金额大小的差别,比较为不同投资者计算的MWR是不恰当的。
当现金流不存在时,收益率被计算为期末市场价值除以期初市场价值。假如投资期内发生了现金流,那么我们需要考虑现金流的金额和发生时间。为了解释现金流的发生时间,我们计算一个加权调整,并用之按现金流的部分投资期调整现金流。以下电子数据表显示了假如我们计算1年期的MWR,并且有两笔现金流,第一笔在1月末发生,第二笔在2月末发生,那么1月末现金流的权重将为92%(现金流在当年92%的时间内可用于投资),2月末现金流的权重为83%(现金流在当年83%的时间内可用于投资)。

内部收益率(IRR)
假设我们在年初投资了$100,并在年末拥有$140。我们在1月和2月末各注入了$10的现金流。这种情形下的MWR收益率是多少?我们寻求的MWR将是解开下列方程的值:
100×(1+MWR)+10×(1+MWR)0.92+10×(1+MWR)0.83=140
将期初价值和期间现金流与期末价值联系起来的收益率是内部收益率(internaI rate of return)或IRR。这个收益率是解得下列方程中的IRR的值:
MVE=MVB×(1+IRR)+CF1×(1+IRR)1…CFN×(1+IRR)N
其中,
CF=进出投资组合的现金流金额
N=CF可用于投资的时期比例
IRR是我们所观察到的市场价值和现金流所隐含的收益率。除了最简单的情形外,我们在所有情形下都不能直接对IRR求解。不幸的是,我们不能利用代数重新排列方程项数以推导出答案。IRR是用试误程序计算的,其中,我们先猜测一个答案,然后根据我们在上一次试验中有多么接近答案用下一个值进行重复试验,直至求得问题答案为止。
人们已发展了有效地执行迭算、以迅速收敛于答案的技术。以下电子数据表显示了利用Excel的求解功能进行的IRR计算:

在这里,我们将单元D5中的期末市场价值与单元E5中的未来价值总额的差额设定为零。接着,我们对单元E8中的IRR求解。这个IRR为17.05%,因为正如以下显示的那样,它是使现金流与期末市场价值一致的利率。
100×(1+0.1705)+10×(1+0.1705)0.92+10×(1+0.1705)0.83=140
注意:IRR公式隐含了一个假设:收益率在投资期内被假设为固定不变。在这个例子中,每笔现金流在整个投资期部分都是以17.05%复合的。
我们可以对小于一年的时期计算IRR。我们对每笔现金流利用的时期权重为我们所考虑的总时期的比例。例如,一笔在一个有31天的月份的第10天发生的现金流将具有当月[(31-10)/31]=0.7097的权重。(这假设了供款是在第10日的一早进行的,如果我们假设现金流是在当日结束时发生的,那么应减去一天。)小于一年的IRR计算结果被解释为测量期内的IRR。以下电子数据表显示了下列情形下的月IRR计算:2000年12月31日的MVB=1000,2001年1月31日的MVE=1200,并且有两笔现金流发生,2001年1月10日有$400进入投资组合,2001年1月20日有$100退出投资组合。

当账户中有提款发生时,我们使IRR中利用的现金流调整为负数。这种现金流模式的一个月期IRR为-8.02%。
IRR的问题
我们将IRR归类为一种MWR,因为它同时考虑到了投资组合现金流的发生时间和金额大小。它是投资者所实现的投资业绩的恰当测度。由于迭算法所用的计算机时间,IRR需要通过迭算法计算的事实曾经使1RR成为一项成本极高的计算。这在今天不成问题。但该历史问题导致了各种低成本地估计IRR的创新方法的发展。这些方法之一——修正迪茨方法(Modified Dietz method)——仍是分析员用以计算MWR并(正如我们将看到的那样)在我们计算TWR时估计不同估值日期间的收益率的常见方法。
修正迪茨收益率
修正迪茨收益率(Modified Dietz return)是MWR的一种单利估计。修正迪茨计算与ROI的计算相同,但添加至期初市场价值的现金流是根据它们投资于投资组合的时间被加以调整的。

其中,
CF=投资期内的净现金流金额
CD=投资期内的总天数
Ci=现金流的发生日
CFi=Ci日的净现金流金额
这则计算以其发明者彼得·迪茨(Peter Dietz)命名,他任职于法兰克·罗素(Frank Russell)养老金咨询公司。原始的迪茨方法假设现金流是在投资期的中途发生的,它如今已不再被加以采用。
为了说明修正迪茨收益率的计算,让我们考虑以下情形。
期初市场价值+应计收益 MVB 100
期末市场价值+应计收益 MVE 120
总和(客户供款/提款) CF 10(在一个30天的月份中的第20天发生)
为了计算以上显示的修正迪茨收益率,我们先在现金流于第20天的末尾发生的假设下计算调整系数,它为0.33。

接着,我们通过将金额乘以调整系数,调整现金流:0.33×$10=$3.33。然后,我们将修正现金流添加到分母中的期初市场价值上,并计算修正迪茨收益率,它为9.68%。
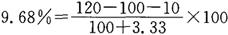
IRR和修正迪茨公式都是资金加权收益率。MWR结果受到期间现金流的发生时间和金额大小的影响。完全消除投资者现金流影响的收益率统计值为时间加权收益率。
投资经理的业绩:时间加权收益率
收益率是资产在某个时期内的百分比价值变化。总收益率是通过将资本利得/损失和赚取的收益除以期初投资价值计算的。正如我们在本章前面看到的那样,根据投资者的现金流进出投资组合的时间和金额大小,投资者在同一基金的投资中会实现不同的收益率。收益率被用以评估投资经理的业绩,但他/她(通常)对投资者现金流的发生时间和金额没有控制权,因此我们需要一个消除这些现金流的影响的业绩测度。理想的收益率将以整个时期内的投资资金的收益率评价投资经理,并消除客户现金流的影响。
时间加权收益率
时间加权收益率(TWR)是一种测量在整个测量期内投资于基金的一美元的业绩的总收益率。TWR消除了投资组合外部现金流的发生时间对业绩的影响,只剩下市场和投资经理决策的影响。
为了计算时间加权收益率,我们将我们感兴趣的时期分为子时段、计算在子时段内赚取的收益率,并复合这些子时段收益率以推导出整个时期的TWR。子时段的界限是每笔现金流的发生日。具体而言,计算TWR的步骤为:
1.从期初市场价值开始。
2.将时间后移到期末。
3.记下紧接在现金流进出投资组合前的投资组合价值。
4.计算在估值日期间的时段的子时段收益率。
5.对我们遇到的每笔现金流重复步骤3和4。
6.当现金流不再出现时,利用期末市场价值计算最后一个时段的子时段收益率。
7.通过计算(1+子时段收益率)的乘积复合子时段收益率。
最后一个步骤被称为收益率的几何关联(geometric linking)或链接(chain linking)。链接具有与在未来价值计算中的复合相同的功能。当子时段收益率在不同子时段内发生变化时,我们利用链接,而不是未来价值公式。
时间加权收益率=[(1+R1)×(1+R2)×…(1+RN)-1]×100
其中,RN为子时段收益率。
TWR假设了我们对在先前的子时段中赚取的收益进行复合和再投资。表达式(1+子时段收益率)被称为财富相对比率(wealth relative rate)或增长率(growth rate),它代表了资本在子时段内的增加。例如,假如投资组合在子时段初的价值为$100,并且在下一笔现金流发生前的子时段末的价值为$105,那么该子时段的收益率为5%,增长率等于1.05。
我们将在下面说明计算TWR的步骤。我们在基金的市场价值如下表所示的情况下计算一个月期的TWR:

当月有两笔现金流:

将时期分割为子时段
TWR计算的第一步是将我们感兴趣的时期分割为子时段,其中子时段是由现金流的发生日分离开来的。下一步是记下在每笔现金流发生前的投资组合价值。假如我们采用的是现金流在日初发生的假设,那么我们利用在现金流发生日的前一个晚上执行的估值。

我们共有两笔现金流和三个子时段。
1.5月31日至6月9日末
2.6月10日至6月19日末
3.6月20日至6月30日末
注意,我们共有(1+现金流发生日的天数)个子时段。
计算子时段收益率
接着,我们计算每个子时段的单期收益率。现金流在一天中的发生时间的假设决定了子时段收益率公式中的现金流处理。在这里,我们假设现金流是在日初发生的。在日初假设下,我们将现金流添加至日初的市场价值上,以形成收益率的分母。进入投资组合的现金流被添加至分母上,退出投资组合的现金流则被从分母中减除。假如一天中有多笔现金流,那么我们计算这些现金流的净额。

假如我们计算的是单位化产品(如共同基金)的业绩,那么子时段收益率公式的输入变量为每股净资产值和红利分配。现金流调整的效果是从收益率计算中消除供款/提款的影响。以下电子数据表显示了三个子时段收益率的计算,10.00%、-7.69%和9.09%。
计算多时段收益率
当月的百分比收益率是通过链接子时段收益率计算的。
[(1.1000)×(0.9231)×(1.0909)-1]×100=10.77%
通过用这种方式计算收益率,我们从收益率中完全消除了现金流进出投资组合的影响。图3.2提供了一个显示TWR是如何从收益率计算中消除现金流影响的方法。

图3.2 时间加权收益率
一般而言,TWR是投资经理业绩的恰当测度,但也有一些例外。在某些情形下,投资组合经理确实对现金流的发生时间拥有决定权。例如,在私募股权基金(第二十六章讨论的一种投资工具)的管理中,一般合伙人在希望投资时会提取投资者承诺的资本。然而,在大多数业绩测量应用中,TWR都是投资经理业绩的恰当测度。
估计时间加权收益率
这个方法的实施有一个潜在障碍。TWR要求我们在每笔现金流发生前评估投资组合的价值。不幸的是,这些定期估值不是总能取得的。例如,大多数机构独立账户都是每月估值的,但客户可以在月中的任何时候在账户中存入或提取资金。尽管行业趋势倾向于每日进行估值,但在我们可以为所有投资工具取得每日估值前,我们需要一个在供款和提款发生于估值日期间时估计真实TWR的方法。
我们可以通过计算估值日期间的每个子时段的MWR,并利用在将子时段收益率链接为TWR时利用的链接方法在更长的时期内复合这些MWR以近似TWR。TWR的这个链接MWR估计在现金流相对投资组合的规模较小、并且子时段内的收益率之波动率较低的情形下提供了TWR的可靠近似。假如现金流金额较大,并且市场在测量期内波动性较高,那么TWR的MWR估计将是不精确的。因此,我们必须指出,链接MWR是在较长时期内的TWR的估计值。尽管现金流在子时段内被赋予了权重,但它们仍会影响收益率。链接过程未从累计收益率的计算中消除现金流的影响。一个计算TWR的折衷方法是在现金流的金额较大时执行特殊估值,然后将子时段MWR链接起来。
表3.1 总结了资金加权收益率与时间加权收益率的差别。
表3.1

多时段收益率的计算
我们可以通过复合单期收益率,计算多时期收益率。我们通常对反映复合功能的定期收益率的平均值感兴趣。平均收益率通常是用年平均收益率重新表述的。本节讨论了这些主题。
累计收益率
我们在链接过程中用子时段收益率创建多时段TWR时看到了复合程序是如何执行的。我们可以同样用这种方法推导出任何时期的累计收益率,如本月至今为止、本年至今为止、一季度、1年期、3年期和从账户起始日起的收益率。为了复合收益率,我们将每个时段的(1+小数收益率)相乘。
累计收益率=[(增长率1)×(增长率2)…-1]×100
以下电子数据表显示了在给定年收益率系列9%、6%、-2%、8%和-4%的情况下,5年期累计收益率的计算。

通过复合收益率,我们求得5年期累计收益率为17.40%。
由于我们通常对不同时期内的投资业绩感兴趣,我们可以保留累计增长率的记录。累计增长率对快速计算多个时期的累计收益率十分有用,因为我们不需要利用期间的收益率或增长率。累计增长率是通过取上一个时期末的累计增长率并将之乘以(1+当期收益率)计算的。我们可以通过将投资额乘以累计增长系数,利用累计增长率计算投资的预期价值。例如,当5年期复合增长率为1.2568时,在基金中投资的$100将生成$125.68的期末价值。
100×(1.2568)=125.68 61
增长率也可被用以推导出任何两个日期间的收益率。

当我们对长时期内的投资业绩感兴趣时,我们计算累计收益率。注意,累计收益率包含了投资收益被再投资于基金、并且被加以复合的假设。每个时期末的增值(用收益率测量)被当作是在下一个时期再投资于投资组合的收益。
压缩时期
单期收益率通常是每日或每月定期计算的。我们可以通过复合将单期收益率压缩为更长期的收益率。例如,在一个月期间计算的每日收益率可以被压缩或“滚动”为月收益率。复合12个月收益率将给出与利用基础的日收益率相同的结果。同样,为了计算多年的收益率,我们可以将月收益率压缩为年收益率。在先前我们说明累计收益率的计算中,我们利用了5个年收益率以推导出5年期累计收益率。假如年收益率实际上是用日收益率计算的,那么我们可以链接1250个(250个交易日×5年)左右的日收益率并得出相同结果。利用压缩的月、季度或年收益率更为简单,即使它们最初是用日收益率计算的。
算术平均收益率
通常,我们对计算投资收益率的平均值感兴趣。我们可用平均收益率比较投资经理或基金在不同时期内的业绩。我们有两个计算收益率系列之平均值的方法:算术方法和几何方法。作为平均收益率的一个测度,我们可以通过将定期收益率相加起来并除以收益率的个数以计算算术平均收益率。

每个收益率的周期都必须相同(也就是说,所有收益率都必须是日、月或年收益率)。我们不能在所有应用中都使用算术平均收益率。例如,我们也许希望利用平均年收益率以预测投资的未来价值。利用算术平均收益率的一个问题是:它们未考虑到收益率在不同时期内的复合。例如,假如我们有两个年收益率:

算术平均收益率为15%[(20+10)/2]。复合的2年期收益率为32%。
[(1.10)×(1.20)-1]×100=32.00%
假如我们取算术平均收益率并将之代入复合公式,我们将得出比利用实际的定期收益率更高的结果。
[(1.15)×(1.15)-1]×100=32.25%
利用算术平均收益率将期初投资价值和期末投资价值联系起来会高估期末价值。为了包含复合程序,我们在这例应用中利用的平均收益率应小于算术平均收益率。
几何平均收益率
当我们将平均年收益率乘以总年数时,结果不等于复合收益率,因为它未考虑到通过对上一时期的收益进行再投资赚取的收益。在上一个例子中,第2年的20%的收益率是通过对第1年的10%的收益进行再投资赚取的,但算术平均收益率未考虑到这点。为了纠正这个问题,我们计算几何平均收益率、而不是算术平均收益率。几何平均收益率是复合收益率的n次方根,其中n为用以计算复合累计收益率的时期数。即:

(注意,计算方根是将增长率相乘的逆反程序。)
以下电子数据表显示了从32%的2年期复合收益率推导而来的几何平均年收益率等于14.89%。
在Exce1软件中,为了求得n次方根,我们取复合增长率的(1/N)次幂。
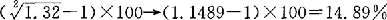
将几何平均收益率代入复合增长率公式将得出当期的复合收益率。
复合收益率={[1+(几何平均收益率/100)]N-1}×100
我们可以利用14.89%的几何平均收益率,重新得出32%的两年期复合收益率。
{[1+(14.89/100)]2-1}×100→[(1.1489)2-1]×100→(1.32-1)×100→32%
或
{[(1.1489)×(1.1489)]-1}×100=32%

下列电子数据表的C栏显示了利用平均收益率的一个好处在于,我们不需要知道实际的定期收益率即可计算未来价值:

将小于1年的收益率换算为年化收益率
无论实际投资期有多长或多短,收益率通常是用年收益率表示的。我们这样做的原因在于:假如每笔投资的投资期是用相同长度表示的,那么投资收益率的比较将更为简单。1年期的几何平均收益率被称为平均年收益率、复合年收益率或年化收益率。
利率通常是用年利率报价的。假如我们有一个小于1年期的收益率并需要将之转换为年收益率,那么我们可以通过取持有期收益率的一年中的时期数次幂以复合这个收益率:
{[1+持有期收益率)时期数]-1}×100
在这种情形中,我们将需要继续对单期利率加以再投资,以产生年收益率。由于这个原因,基于小于1年的累计期计算的年化收益率是年收益率的假想预测。作为用这种方法计算的年收益率之问题的一个极端例子,假设市场在某一个月份的表现极佳并上升了20%。将之换算为年收益率将产生792%的复合年收益率。
对小于1年的持有期计算的年化收益率将被解释为在当年剩余时期的业绩与当年至此为止已实际经历的业绩相同的假设下的当年收益率水平。
将大于1年的收益率换算为年化收益率
假如我们换算为年化收益率的多期复合收益率是对大于1年的时期计算的,那么我们利用复合公式的逆反方程将复合收益率重新表达为年收益率。取一个数的n次幂的逆反程序是取这个数的n次方根。

例如,假如一项投资在3年时期内赚取了19.1%,我们可以通过求累计增长率的三次根,得出6%的年平均收益率。
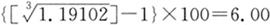
注意,我们通过取累计增长率、而不是累计收益率的n次方根计算年收益率。增长率的n次方根是几何平均增长率。为了将平均增长率转换为几何平均收益率,我们减除1并乘以100。
我们通常需要计算非整数年数的累计期的年化收益率。为了计算这些非整数时期的年化收益率,我们可以计算累计期内的实际日历天数,并将之除以365.25以计算等价的年化收益率。

例如,与在16个月内赚取的14%的收益率等价的年化收益率等于10.37%。
复合年内部收益率
假如我们利用的是在大于1年的时期内计算的美元加权IRR,那么我们也可以计算等价的年IRR。为了做到这点,我们调整用以将现金流与期末市场价值联系起来的权重,以使它们为1年的倍数。以下电子数据表显示了与10.00%的5年期IRR等价的年IRR的计算:

这等价于1.93%的年IRR。注意,我们用5年的权重加权期初投资余额,用4年加权第一笔现金流,以此类推。
总结
在本章中,我们概述了计算投资收益率和解释投资收益率的含义的程序。我们将定期的投资组合估值和现金流数字转换成了单期收益率。时间加权收益率测量了归因于投资经理的业绩。美元加权收益率同时反映了投资经理的业绩和投资者交易的时机。
收益率是对投资业绩的一个方面的描述。业绩测量还关系到测量为赚取这些收益率所承担的风险,以及如何将收益率归因于市场活动和主动式管理。随着投资周期的演变,我们在业绩测量中计算的收益率、风险和归因统计数据将成为下一轮的资产配置和证券选择决策中的输入变量。
【作者信息】:雄鹰投资系统公司业绩测量技术主管