球面构件的计算展开
出处:按学科分类—工业技术 河南科学技术出版社《钣金技术手册》第461页(5211字)
(一)小型三瓣球体构件的计算展开
图6-60a为装饰用不锈钢球体。根据其尺寸和制造工艺要求,球体等分成三块瓜瓣且分别成型,再拼接成整体。因此,每块瓜瓣须计算展开的具体方法如下:

图6-60 小型三瓣球体的计算展开(单位:mm)
a.主视图 b.顶圆展开图 c.1/3瓜瓣展开图
1.有关参数的计算
即顶端展开半径R0、顶圆处纬圆半径r、瓜瓣上端1/2弧长S1中部1/2弧长S2、上端弦高e和半弦长B0,以及纵向弦长B等参数的计算如下:
R0=Rtan30°=247.5×tan30°=143(mm)
r=Rsin30°=247.5×sin30°=124(mm)

S2=πr/n=π×247.5/3=259(mm)
展开料上端所对半圆心角α1:

e=R0×(1-cosα1)=143×(1-cos51.92°)=54.8(mm)
B0=R0sinα=143×sin51.92°=112.6(mm)
2.展开尺寸的计算
(1)瓜瓣料长的计算:

(2)瓜瓣侧弧弧长及半径的计算:
B=L+2e=518+2×54.8≈628(mm)
根据相交弦定理可得
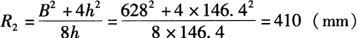
(3)顶圆直径的计算展开:
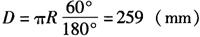
(二)大型球罐构件的计算展开
图6-61为橘瓣式球形贮罐,球壳由对称分带分块拼焊而成,其已知尺寸和计算原理如图6-61b所示。

图6-61 1000m3橘瓣式球罐的计算(单位:mm)
a.主视图 b.计算原理图
1.赤道带的计算展开
(1)相关参数计算:如图6-61b和图6-62a所示,需计算的相关参数有半纵向中心弧长l1、纵向每等份弧长y、每等份所对球心角Q′1、各等分点所处截圆半径Rn和各等分点横向弧长Sn等,计算如下:

图6-62 1000m3橘瓣球罐展开(单位:mm)
a.赤道带展开图 b.温带展开图 c.极带中央板展开图 d.极带边板展开图
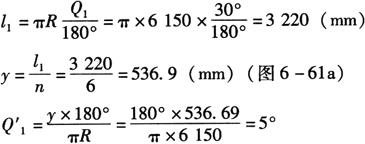
Rn=RcosQ′1
其中 R1=6150mm,R2=6126.6mm,R3=6056.6mm,R4=5940.4mm,R5=5779.1mm,R6=5573.8mm,R7=5320.1mm。

赤道带纵向分十二横向瓣片,每片球心角为30°,得S1=3220mm,S2=3207.9mm,…,S6=2918.4mm,S7=2788.7mm。
(2)展开尺寸计算:如图6-61和6-62a所示,上口展开半径RO1、上端弧所对顶角α7和弦高e7的计算如下:
RO1=Rtan(Q2+Q3)=6150×tan60°=10652.1(mm)
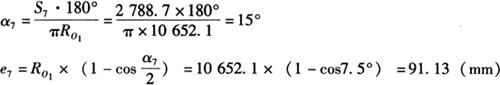
2.温带的计算展开
(1)相关参数计算:如图6-61b和图6-62b所示,相关参数有纵向中心弧长l2、纵向角等分弧长y、每等份所对球心角Q′2、各等分点所处截圆半径Rn及各等分点横向弧长Sn等,计算如下:
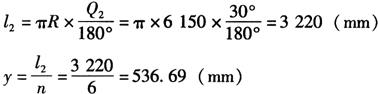

其中 R7=6150×cos30°=5326.1mm,R8=6150×cos35°=5037.8mm,R9=4711.2mm,R10=4348.7mm,R11=3953mm,R12=3527.5mm,R13=3075mm。

同理,得S8=2637.8mm,S9=2466.8mm,S10=2277mm,S11=2069.8mm,S12=1847mm,S13=1610mm。
(2)展开尺寸计算:如图6-61b所示,上口展开半径RO2、上端弧所对顶角α13、上口弦高e13的计算如下:
RO2=RtanQ3=6150×tan30°=3550.7(mm)
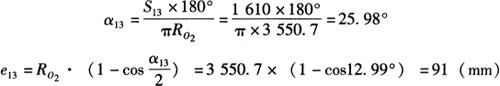
3.极带中央板的计算展开
相关参数如半纵向中心弧长l4、纵向每等份弧长y、每等份所对球心角Q、各等分点所处截圆半径为Rn、各等分点横向弧长Sn及端口半径RO2和边沿半弧长l″4等(图6-62c),计算如下:

其中 R1=6150mm,R2=6150×cos5°=6126.6mm,R3=6056.6mm,R4=5940.45mm,R5=5779mm,R6=5573.8mm,R7=5326mm。

其中 Q″3=13°,S1=2790.8mm,S2=π×6126.5× =2780.2mm,…,S6=2529.3mm,S7=2416.9mm,RO2=RtanQ3=6150×tan30°=3550.7(mm)。
=2780.2mm,…,S6=2529.3mm,S7=2416.9mm,RO2=RtanQ3=6150×tan30°=3550.7(mm)。

4.极带边板的计算展开(图6-62d)

其中 R2=6150×cos4.55°=6130.5mm,R3=6072.7mm,R1=6150mm,R4=5976.6mm,R5=5842.9mm,R6=5672.4mm,R7=5466.2mm。

其中 S2=π×6130.5×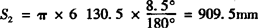 =909.5mm,S1=912.4mm,…,S6=841.5mm,S7=811mm。
=909.5mm,S1=912.4mm,…,S6=841.5mm,S7=811mm。
5.右边板的计算

y、Q、Rn值均同左边板的计算结果,但其各横向弧在其截圆上的圆心角λn各异,Sn也不同左边板需计算。

 -(13°+8.5°)=8.19°
-(13°+8.5°)=8.19° 同理,得λ3=7.21°,λ4=5.48°,λ5=2.78°,λ6=-1.38°,λ7=-8.5°。
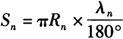
 =912.4(mm),S2=875.8(mm),…,S6=136.3mm,S7=811mm。
=912.4(mm),S2=875.8(mm),…,S6=136.3mm,S7=811mm。 6点与中心线距离:
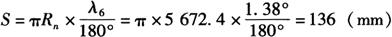
(三)旋转体拉深构件的计算展开
拉深是一种比较复杂的成型工艺方法,用拉深方法制成的工件形状也较复杂。拉深时,材料的平面尺寸、厚度及形状都发生变化,成型后还需修边,所以坯料的尺寸计算也较复杂。
由于形状简单的旋转体拉深件的坯料为圆形,故尺寸计算可采用等面积法。
虽然在拉深中毛坯的厚度将会有一些变化,但对于一些形状简单、要求不太高的拉深件,可以不计毛坯厚度的变化,粗略地以拉深前后面积相等进行计算。
在计算时,首先将拉深成型的旋转体工件划分成若干个便于计算的组成部分,分别求出各部分的面积。然后将各部分面积相加求和,得到工件的总表面积∑F。最后按下式计算出圆形坯料直径:
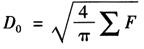
式中 D0——坯料的直径(mm);
∑F——拉深件的总表面积(mm2)。
1.筒形拉深件的尺寸确定
如图6-63a所示,为便于计算,将筒体划分为圆柱面、转角部和圆底部三部分,各部分的外表面积可方便地计算出来。

图6-63 旋转体拉深件的计算展开
a.筒形件坯料的尺寸 b.椭圆形封头的尺寸
(1)圆柱面:
F1=πd2h
(2)转角部:

(3)圆底部:

(4)总外表面积:

将∑F代入上述D0
式中,进行整理化简后,得坯料直径为
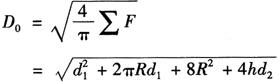
根据等面积计算原则,一些常用旋转体拉深件坯料计算公式列于表6-2。
表6-2 常用旋转体拉深件坯料直径的计算式(mm)



2.椭圆形封头的尺寸计算
椭圆形封头是各种压力容器所必备的零件,它属于曲面形状复杂、技术要求较高的拉深件,如图6-63b所示,其坯料直径可用近似计算法或经验公式法确定。
(1)周长法:周长法是一种近似计算法,按下式确定坯料直径:
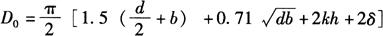
式中 D0——坯料直径(mm);
d——封头内径(mm);
b——封头椭圆部分高度(mm);
h——封头直边部分高度(mm);
k——封头压延系数,通常取k=0.75;
δ——修边余量(mm)。
(2)等面积法:等面积法是另一种近似计算法。这种方法是以封头中性层的面积等于坯料面积来计算坯料尺寸。对于标准椭圆封头(b=d/4),坯料直径可按下式计算:

式中 t——封头壁厚(mm)。
对于非标准椭圆封头,坯料直径可按下式进行近似计算:
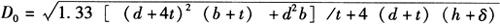
(3)经验公式法:对于b=d/4的标准椭圆封头,坯料直径还可按以下经验公式计算(式中已经包含修边余量):
D0≈d+b+h