晶体生长理论——二维成核学说

出处：按学科分类—工业技术 中国轻工业出版社《制盐工业手册》第312页（1101字）

表面反应过程常常是晶体生长过程的控制阶段。解释晶体表面反应机理的一个重要学说是二维成核学说：“一个真实的晶体可以被想象为一个立方体，由许多小立方体堆砌而成，各小立方体可认为是微小的粒子，也可以是原子、分子、离子或分子团。每个小立方体有6个近邻，有6个面彼此接触。当一个新粒子添加到晶面上时，可能性最大的位置应该是能量最有利的位置，或者说是成键数最多的位置。”

由图2－5－17可见，最有利的添加位置是台阶的缺口(kink)，如立方体(1)处，它有3个近邻，可以成键；第二个有利的位置是台阶的前缘，如立方体(2)处；最不利的位置是晶体表面上孤立的粒子位置，如立方体(3)处。完整晶面上既无台阶，更无缺口，形成新的粒子层只有从最不利的位置开始，当有一个粒子加到晶面上后，其他粒子就会迅速地加到台阶前缘或缺口处，而形成整个粒子层。最先加到晶面上的粒子可认为是一个二维生长的核，它是新晶层形成的开始。晶体的生长速率取决于晶面上二维生长的核的形成速率。二维成核的动力学方程式为：

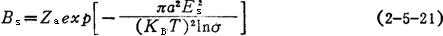
式中 B_S——表面成核速率〔数目／(〔m²·s)〕

Z_a——表面处新粒子到达的速率〔数目／(cm²·s)〕

K_B——Boltzman常数〔1．3806×10^－16erg／(mol·k)〕

a²——单个粒子覆盖的面积(cm²)

E_s——界面能(erg／cm²)

σ——相对过饱和度

图2－5－17 部分完成的晶体表面

根据上式所表达的二维成核定律，在低过饱和度范围内的晶体生长速率如图2－5－18中实线ab段所示。概括地说，只有过饱和度超过某一限度(如图中a点)，生长始能进行；b点以上，生长速率与过饱和度近似地呈线性关系，因为在较高的过饱和度下，粒子碰撞晶面的频率已很高，表面生长的核经常存在。但大多数晶体的实际生长速率，却如图2－5－18中虚线所示，随所有过饱和度(包括低过饱和度)呈线性增长。

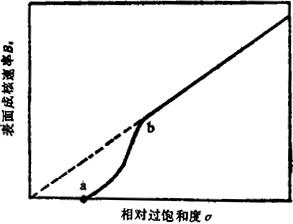
图2－5－18 二维(表面)成核速率与相对过饱和度的函数关系图