基本原理
出处:按学科分类—农业科学 农业出版社《土壤农化分析手册》第68页(2838字)
(一)共振发射线和吸收线 根据玻尔氢原子理论,由氢原子能级图说明:

图2-11 氢原子的能级图
(1)电子有基态、激发态和离子三个能级,激发态又有n=1至n=∞的许多能级;
(2)处于基态的电子,在轨道上运动,没有辐射产生;
(3)当电子获得能量跃迁时,才产生辐射。辐射为一系列不连续值,所以原子光谱为线光谱,并且是负值。即电子须获得一定能量才可跃迁。见图2-12。

图2-12 电子跃迁示意图
h——为普朗克常数=6.63×10-34J·s
v——为频率
举例说明:H原子中电子由E3跃迁至E2则


则

又因为

则

注释:

而当跃迁返回时,就发射光量子即发射光波,此光波有一定的波长。一个原子有许多许多发射线,这就构成原子的线光谱。光电子从第一激发态跃迁回基态时,所发射的谱线称为该元素的共振发射线。共振线是由基态原子吸收入射光电子跃迁仅达第一激发态(即能量最低的激发态)时退激过程所产生的。一般为时一瞬仅10-8s。一定的原子体系吸收其相应原子发出的共振发射线,称为该元素的共振吸收线(共振吸收线常常在更广泛的含义下使用,即凡是由基态引起的跃迁吸收线,不管它上面能级的位置如何,都可叫共振线)。原子吸收分光光度法首先须共振线,才能使待测基态元素吸收能量,产生吸收跃迁谱线。所以原子吸收光谱现象虽早已发现,但只有在获得发射共振线的空心阴极灯后,才有可能利用这一原理测定元素。
(二)原子对共振发射线的吸收,符合朗伯—比尔定律

公式中:Iv——吸收后频率为v的光强;
Iov——光源频率为v的光强;
e——自然对数;
Kv——吸收系数;
C——原子浓度;
L——火焰厚度。
将上式化为:

也即是发射光强和吸收后光强弱的对数与原子浓度、通过原子火焰厚度在一定范围内成直接关系。
但Iov发射线和Iv吸收射皆不可能是一条细线,而实际是一个面,其形状图2-13所示。横轴为频率v,纵轴为吸收系数Kv,一般谱线的“半宽”△v来表述其宽度特征。当很多原子共同存在时,由于外界条件及其本身的互相影响造成原子吸收的微扰,使其不可能仅仅吸收对应于v0的一条线,而是具有一定的宽度。这样,凡是影响谱线宽度的因素,必然对原子吸收法产生各种影响。一般有以下几种。
1.自然宽度(以△vN表示) 它与电子在原子内部的振动受到阻尼有关。对共振线来说,其自然宽度一般在10-2-10-4数量级。与其他变宽比较,在原子吸收中自然变宽可以不预考虑。
2.多普勒(Doppler)变宽(以△vD表示)或称温变宽 它与相对于观察的原子无规则热运动有关。

图2-13 吸收线的形状图

式中:A——为元素的原子量;
T——为绝对温度。
所以在一定范围内,温度的微小变化对谱线宽度的影响并不很大。但从式中可见,待测元素的原子量A越小,温度越高,则谱线的多普勒变宽越大。所以对原子量小的钠,不如用火焰法,而少用原子光谱法。
3.劳伦茨(Lorentz)变宽(以△vL表示) 吸收原子与外界气体分子间相互作用引起此种变宽,故又称为压变宽。火焰喷雾原子化时,压变宽是主要的,一个大气压引起变宽约在0.01-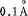 范围内,表2-4是
范围内,表2-4是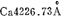 线的变宽。
线的变宽。
(三)基态原子与激发态原子 待测化合物溶液在火焰原子化时,是否皆以基态原子存在?还是也有激发态原子?这是影响原子吸收分光光度法准确度的问题。
表2-4  线的变宽
线的变宽

当绝对温度T达到温度平衡时(即等温状态,热力学平衡的条件下),激发态与基态原子数目的比值,原子按能级分布,可近似服从波茨曼(Boltzmann)分布定律,由公式表示如下:
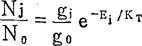
公式中:Nj,N0——分别为激发态、基态原子数目;
gj,g0——分别为激发态、基态的统计权重(统计权重是指粒子在某一能级下可能具有的几种不同状态数);
e——自然对数;
Ej——激发能量;
K——波茨曼常数=1.38×-18尔格/度;
T——绝对温度。
在原子光谱学中,Pj/P0及Ej都是已知,所以只要确定火焰温度T后,就可以求出Nj/N0值。
在常用温度2000-3000°K范围,大多数化合物可成原子态,其中可能有部分为激发态,也即火焰中的原子有基态,也有激发态。由表2-5可见,最低激发态的原子数与基态原子数的比值是比较小的。如3000°K时,Ba的比值只有10-4左右,因之Nj比N0小到可以略而不计。火焰中基本上是呈基态原子状态存在的。火焰温度稍发生改变,Nj就发生较大的变化,但对N0的影响都很小,因此,原子吸收分光光度法可获得较好的稳定性。
表2-5 温度对各种元素共振线的Nj/N0比值的影响
