钝角

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第85页（2671字）

大于90°而小于180°的角叫做钝角．

例1 ①37°48′+45．36°=＿＿．

②47°－14°24′=＿＿．

③34．37°=＿＿度＿＿分＿＿秒．

④11°24′36″=＿＿度．

答 ①83．16°，②32°36′，

③34，22，12，④11．41．

[解析] ①单位不统一，须化成统一单位37°48′=37．8°．

②把47°转化成46°60′．

③整数部分保留，小数部分向下一级单位转化．

34．37°=34°+0．37°=34°+0．37°×60′

=34°+22．2′=34°+22′+0．2×60″

=34°+22′+12″=34°22′12″．

④11°24′36″=11°+24′+[36×(1/60)]′

=11°24′0．6′=11°+24．6′

=11°+24．6′×(1/60)°=11°+0．41°

=11．41°．

例2 一个钝角与一个锐角的差( )．

A．一定是钝角 B．一定是直角

C．一定是锐角 D．不能确定

答 D．

[解析] 若钝角为130°，锐角为20°，则差为钝角110°．

若钝角为130°，锐角为50°，则差为锐角80°．

若钝角为130°，锐角为40°，则差为直角90°．

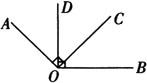
例3 如图所示，AO⊥OC，OD⊥OB

∠COD=38°，则∠AOB=＿＿，

因为∠AOC=∠BOD，所以∠AOC＿＿=∠BOD＿＿，就是∠AOD=∠BOC．

答 142°，∠COD，∠COD．

[解析] ∵∠BOD=90°，∠COD=38°．

∴∠BOC=90°－38°=52°．

∴∠AOB=∠AOC+∠BOC=90°+52°=142°．

例4 右图是七巧板拼成的猫的图案，在这个图案里钝角有( )．

A．0个 B．1个

C．2个 D．3个

答 D．

例5 共顶点的三个角，它们的和刚好是周角，则它们可能都是( )．

A．锐角 B．直角

C．钝角 D．平角

答 C．

[解析] 对于A三个锐角之和小于180°．

对于B三个直角之和为270°．

对于D三个平角之和为540°，故选C．

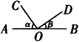
例6 如图，点O在直线AB上，OC⊥OD，若∠α=55°，那么∠β=＿＿．

答 35°．

[解析] ∠AOB是1平角180°．

∠COD=90°，

所以∠α+∠β=90°，

即∠β=90°－∠α=90°－55°=35°．

例7 ①时针在8点整时，其时针与分针所成角的大小为＿＿．

②8点30分，这一时刻分针与时针的夹角是＿＿．

答 ①120°，

②75°．

[解析] 表针转一周是360°，表盘上共有12个大格，60个小格，所以钟面每个大格对应360°÷12=30°的角，每个小格对应360°÷60=6°的角，因此，时针每走1小时对应30°的角，每走一分钟对应30°÷60=0．5°的角；分针每走一小时对应360°角，每走一分钟对应360°÷60=6°的角．

①8点整，时针与分针相差4个大格，4×30°=120°．

②8点30分，时针与分针相差2个大格，另加2．5个小格．因此时针与分针成的角度为2×30°+2．5×6°=75°．