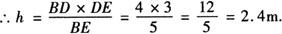梯形中常添加的辅助线

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第128页（4084字）

1．平移腰：过上底的一个顶点作一条腰的平行线，把梯形转化成一个三角形和一个平行四边形．如果是等腰梯形的话，那么三角形就是等腰三角形，它的底边是梯形上下底的差．

例1 以线段a=16，b=13为梯形的两底，以c=10为腰，则另一腰长d的取值范围是＿＿．

答 7

[解析] 过D作DE∥AB交BC于E．

由题意可知：AD=13，AB=10，BC=16．

∵四边形ABED为平行四边形，∴BE=AD=13．

∴DE=AB=10．

∴CE=BC－BE=3．

在△CDE中，根据三边关系定理可知第三边CD的范围在7～13之间．

故7

例2 如图，在梯形ABCD中，AD∥BC，∠B+∠C=90°，AB=4cm，CD=3cm，求BC－AD的值是多少?

解 过A作AE∥DC交BC于E点，

则∠AEB=∠C，AE=CD=3cm，AD=EC．

又∵∠B+∠C=90°，

∴∠B+∠AEB=90°．

即△BEA为直角三角形．

由勾股定理可知BE=5cm，

所以BC－AD=BC－EC=BE=5cm．

2．作高：过上底的顶点向下底引垂线，把梯形转化成两个直角三角形和一个矩形．如果是等腰梯形的话，那么这两个直角三角形全等．

例1 等腰梯形的上底、下底和腰分别为4cm，10cm和5cm，则梯形的高为＿＿，面积为＿＿．

解 如图，分别过点A，D作AE⊥BC，DF⊥BC，则有：BE=CF=3cm，所以AE=(cm)．

所以梯形的面积为：

1/2×(4+10)×4=28(cm²)．

例2 如图，在梯形ABCD中，已知AD∥BC，BC=BD，AD=AB=4cm，∠A=120°，求梯形ABCD的面积．

解 过A作AE⊥BC于E，作DF⊥BC于F，

∴AE∥DF．

又∵AD∥BC且∠A=120°，

∴∠ABC=60°，AE=DF．

∵AB=AD=4，

∴∠ABD=∠ADB=∠DBC=30°．

在Rt△ABE中，得．

在Rt△BDF中，．

∴．

∴S_梯形ABCD=1/2(AD+BC)·AE

=(12+4)cm²．

3．延长两腰：把两腰延长交于一点，把梯形转化成两个三角形，如果是等腰梯形的话，那么这两个三角形就是等腰三角形，其中梯形的上下底分别是两个等腰三角形的底边．

例 在梯形ABCD中，AD∥BC，AB=DC，∠B=60°，BC－AD=6，求腰长AB．

解 延长BA、CD相交于点E．

∵AB=DC，

∴∠B=∠C，∴EB=EC．

又∵∠B=60°，

∴△EBC是等边三角形．

又∵AD∥BC，∠B=60°，

∴∠EAD=∠EDA=60°．

∴△EAD是等边三角形．

∴AB=EB－AE=BC－AD=6．

4．平移对角线：过上底的一个顶点，作一条对角线的平行线，与下底的延长线相交，把梯形转化成一个平行四边形和一个三角形，如果梯形是等腰梯形的话，那么这个三角形就是等腰三角形，它的底是梯形上下底的和．

例1 已知：梯形ABCD中，AD∥BC，对角线AC⊥BD，求证：(AD+BC)²=AC²+BD²．

证明 过D点作DE∥AC交BC的延长线于点E．

又∵AD∥BC，

∴四边形ACED为平行四边形．

∴AD=CE，AC=DE．

又∵AC⊥BD，DE∥AC，

∴DE⊥BD．

∴△BDE是直角三角形．

根据勾股定理，得

BE²=DE²+BD²=AC²+BD²，

即(AD+BC)²=AC²+BD²．

例2 有一块梯形的钢板，标明的尺寸如下：

上底1m，下底4m，对角线AC，BD的长分别为3m和4m，工人师傅想知道它的高，但忘了带测量工具，你能告诉工人师傅这块梯形钢板的高吗?

解 方法：过D作DE∥AC交BC延长线于E．

∵AD∥BC，

∴四边形ACED为平行四边形．

∴AD=CE=1m，AC=DE=3m．

∵BC=4m，

∴BE=5m．

在△BDE中，BD=4m，DE=3m，BE=5m．

∴△BDE为直角三角形，∠BDE=90°．

∴BD×DE=BE×h．

所以这块梯形钢板的高为2．4m．

5．连接上底的一个顶点与另一腰的中点并延长，与下底的延长线相交，得到两个全等的三角形．

例 如图所示，在梯形ABCD中，AD∥BC，AB=AD+BC，E是CD的中点，求证：AE⊥BE．

证明 延长AE交BC的延长线于F．

∵AD∥BC，∴∠D=∠ECF．

又∵∠AED=∠FEC，DE=CE．

∴△ADE≌△FCE．

∴AD=CF，AE=EF．

∵AB=AD+BC，

∴CF+BC=AB=BF．

∴△ABF为等腰三角形．

∵AE=EF，

∴BE⊥AE．(等腰三角形三线合一)