预测误差
出处:按学科分类—自然科学总论 山东人民出版社《方法大辞典》第448页(924字)
预测值与实际值(或观测值)的偏离。
任何预测方法的基本假设都是将某种模式加上某种随机影响,以确定实际预测值。这可写成:
实际值=模式+随机性
因为在任何不可控制的变量中,永远存在不确定性,可以而且也总是伴有随机性。这意味着,即使在基本数据的精解模式已被识别的情况下,在预测值和观测值之间,仍然会存在某种偏离或偏差。
如果X为实际极值, 为预测数值,则误差
为预测数值,则误差 。误差σ在实际值X中所占的百分数称为相对误差ε。
。误差σ在实际值X中所占的百分数称为相对误差ε。

一般地说,可以用σ和ε来表征预测精度。
影响预测精度的主要因素是基础资料、预测方法和相关领域基本理论的熟悉程度。
测定或计算预测误差一般有两种方法:
一种方法,是利用一整套历史数据将一种预测方法与该情况拟合,然后测量实际值与预测值之间的误差。
简单的方法是将几个时间间隔上的误差加起来计算,但是,有时简单相加得出平均值,可发现误差接近于零,这是因为许多正的误差抵消了负的误差。为了避免这个问题,一般可计算平均误差(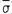 )、平均绝对误差(MAE)、均方误差(MSE)等,它们的计算公式如下:
)、平均绝对误差(MAE)、均方误差(MSE)等,它们的计算公式如下:

另一种方法,是将预测方法仅与一部分现有历史数据拟合,即将现有数据分成两组,应用第一组数据来确定所选择的预测方法的参数,然后将这种预测方法应用到第二组数据上以检验其精确度。由于确定参数时没有应用第二组数据,这就等于对预测方法精确度的事后检验,但这种方法的缺点是没有利用全部数据点,使这种预测方法丧失了本来可用的许多信息,甚至有时由于第二组数据点可能不足以代表未来会发生的情况,出现错误判断的危险,较好的办法是把数据分作两组作误差分析,而根据用于预测目的的全部数据确定参数,建立方程。