拉姆齐增长模式
出处:按学科分类—经济 经济科学出版社《西方经济学大辞典》第430页(3406字)
拉姆齐1928年发表储蓄的数学理论一文,奠定了最优积累和最优增长理论研究的基础。
正如凯恩斯评价说:“(这篇文章)无论在主题本身的重要性及难度方面,运用技巧方法的力度和优美方面,还是在阐述主题的清晰、简洁,使读者了解作者的思想方面,都是对数理经济学所作过的最卓着的贡献之一。”在该文中,拉姆齐的一个突出贡献是,推导出在一个国家的收入中,最优储蓄的简单法则,亦即是现在着名的凯恩斯-拉姆齐法则。这一法则规定:储蓄率乘以货币(或消费)的边际效用,应该等于效用的总净享乐率与最大可能的享乐率之差。
一、拉姆齐模式的基本假定和基本框架
假定社会人口不变,其对享乐能力或对劳动的负效用不变;不同时间的享乐和牺牲互相独立且是可加的;假定没有新发明或组织的改进;假定没有效用的贴现;假定消费和劳动在社会成员之间的分配方式只取决于其总量,因此总满足只是这些总量的函数;忽略不同商品和不同劳动之间的差异;不考虑对外贸易和借贷;最后假定社会的积累动机不变。
令C(t)和L(t)分别为社会的总消费和总劳动,在t时的资本为K(t)。其收入(即产出)是劳动和资本的一般化的函数,即F(K,L)。
由储蓄加消费必等于收入可得:
dK/dt+C=F(K,L) (1)
令U(C)为消费C的总效用率,V(L)为劳动的总负效用率,则相应的边际率u(c)、v(l)分别为:
u(c)=dU(C)/dC; v(l)=dV(L)/dL,假定u(c)从不递增,v(l)从不递减。给定资本K,则U(C)-V(L)表示每单位时间的净享乐,它是资本K的函数,并随资本的增加而增加,因为拥有更多的资本就能取得更多的享乐。然而,享乐率随资本量的增加而递增的趋势终究会终止,这是因为:其一,进一步增加资本并不能提高收入或闲暇;其二,社会已经达到最大的可想象的享乐率,因此更多的收入或闲暇毫无用处。在其中的一种情形下,有限的资本会带来经济上可获得的(obtainable)最大的享乐率。在另一方面,随着资本的增加,享乐率可能永不会停止增长,其原因是:首先,享乐率要么会增加到无穷,要么会渐近于某个有限极限。其二,渐近于有限极限的享乐率可能或不可能等于最大的可想象的享乐率,这一极限称之为最大的可获得的享乐或效用率,简称极乐(Bliss)或B。
由此可见,每一个社会必须充分储蓄以在有限时间达到极乐或至少渐近于极乐。但并不意味整个收入应全部用于储蓄。储蓄越多,就能更快地达到极乐,但现在的享乐就越少,因而两者是替代的。
进一步地,拉姆齐建立起劳动负效用的等式,即任何时刻的劳动的边际负效用等于劳动的边际产出乘以该时刻消费的边际效用:
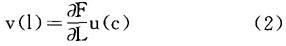
而消费的边际效用等于:

给定初始资本,初始时间t=0,可解得:
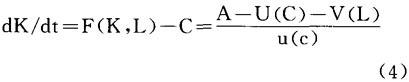
A就是极乐B表示享乐与极乐之差在长期中的积分。它是有限值,问题是使其极小化。改变独立变量K,可得:
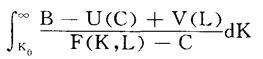
现在C和L都是K的任意函数,极小化这个积分即是使这个积分的偏导数为零。求关于C的导数可得:
-u(c)/[F(K,L)-L]+[B-U(C)+V(L)]/[F(K,L)-L]2
整理可得:
dK/dt=F(K,L)-C=[B-U(C)+V(L)]/u(c) (5)
这就是拉姆齐所推导出来的凯恩斯-拉姆齐法则:储蓄率乘以消费的边际效用应总等于极乐减实际享受的效用率。
运用这个法则,拉姆齐推断,最优储蓄应大大超过人们通常提出的储蓄率。
他举例说明,最优储蓄应为收入的60%。当然,拉姆齐也意识到这个数字可能有问题,他补充说,人口的增加可能使所要求的储蓄更高;未来发明可能使极乐水平比现在的水平更高。另一方面,未来发明和组织的改进可能使未来能以较少的牺牲获得收入,从而可以较少储蓄。
发明有正反两方面的影响:如果我们预先储蓄,它们就会给予我们可以更好满足的新需求,但它们也提高生产性能力并使初始储蓄重要性较小。
这个法则的两个显着特征是:首先它不依赖于生产函数F(K,L);其次,储蓄水平不依赖于现期利率,除非它实际上为零。其实,第一个特征仅仅表面上如此,因为在方程(5)中,C将依赖于产出水平F,而由于方程(5)右边给出的储蓄也依赖于C,所以储蓄水平依赖于F。拉姆齐在其论文的第三部分指出,刺激储蓄水平的动机是对未来消费的需求,利率则由现在的资本存量决定。
二、利率的决定
首先决定每个人以不变率ρ贴现其自身或其后代的效用,那么在均衡状态中就没有储蓄,并且:
dC/dt=dK/dt=0
由此,可得:

这三个方程可以决定C、L和K。最后一个方程表明,决定于资本边际生产率的利率必须等于贴现率ρ。
但如果假定在给定时间内,#,就不存在均衡,但储蓄,因为巨大的数量不可能在短时间内储蓄起来,可能要花几个世纪才能达到均衡,或者永远无法达到,只是渐近于它。同时,问题是,因为利率不是由通常的供给和需求的均衡方程决定的。
利率是如何决定的?拉姆齐指出,利率函数是整个资本存量的需求价格,但作为供给价格则不是针对资本存量而言,而是针对储蓄率。进而拉姆齐强调,“在社会主义国家的会计学上,利率的作用是保证现存资本最聪明地使用,而不是以任何直接的方式来指导收入中储蓄应占的比例。”
拉姆齐模式的主要贡献在于,提出了一个富有成效的问题:一个最优储蓄率是多少?并提供了解决问题的分析方法-动态最优技术,以使跨时效用极大化。除此之外,拉姆齐模式还包括种种内容上的扩展。
它考虑了面临不变要素价格的个人,在希望最优化其终生消费格局时的储蓄率选择,从而提出了确有助益的生命周期储蓄理论。它指出如果考虑效用贴现,那么,为了逃避“后代也受到同样偏好机制激励”这样一个矛盾,人们必须以恒定的贴现率进行贴现。最后,拉姆齐在论文中还证明,如果一个社会是由具有不同贴现率的个人组成,那么均衡可以通过将社会分成两类人而获得。这两类人:一类是享受极乐的富人,一类是维持基本生活水平的穷人。
总之,拉姆齐描述了由相异个人组成的社会长期一般均衡所具备的特征。
由此,拉姆齐奠定了最优积累和最优增长研究的基础,并确立了储蓄和利率的建设性理论。
更具有一般意义的是,拉姆齐模式标志着古典静态分析方法的重大发展,它使资本积累的非静态时间路径分析成为可能,尽管拉姆齐模式最终仍是趋于静态。随着时间的变化,尽管拉姆齐所致力的中心问题-储蓄和投资的正确水平-已失去人们对其的兴趣,但是他所强调的跨时最优化理论的精髓却有强大的生命力,在80年代兴起的内生增长理论研究中大放异彩。