欧拉和力学的变分原理

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第134页（3487字）

欧拉(Leonhard Euler，1707～1783)在经典力学发展中的历史功绩，在于将数学分析方法应用于力学问题。

分析力学这门科学是以少数假定为基础，由这些假定出发，导出物体的平衡和运动的全部规律。目前，力学的变分原理是分析力学的基础，也就是数学上用变分关系的形式表示的基本的、原始的规则，力学的全部运动微分方程和定律都是作为变分原理的逻辑结果。

各种变分原理，无论在形式上及变分手段上，还是在共同性上，都彼此不同，但每一个原理在其可应用范围内都是一个基础，并且好像综合了相应物质系统的整个力学。

变分原理在形式上可分成表征任何给定时刻运动的微分原理和表征任何有限时间间隔运动性质的积分原理。

欧拉主张以基本微分原理之一，即现今知道的达朗伯－拉格朗日(D’Alembert-Lagrange)原理作为起源，并首先在数学上给出了最小作用量积分原理的严格的富有成效的表述，其更一般的研究由拉格朗日和雅可比(Jacobi)继续和完成。

力学的变分原理促进了与其相关的强有力的数学形式体系，拉格朗日和哈密顿(Hamilton)形式体系的发展，它们与力学中的变换问题，李(Lie)群守恒律及其它基本问题密切相联系。

欧拉最初的大量工作花费在力学上，1736年在彼得堡发表了他的《力学，或者说用分析描述运动的科学》着作，在这个工作中欧拉以合理的形式建立了点的运动方程并系统地用它们解决了许多问题。

为解一系列振动理论问题，欧拉(1740)将雅·伯努利－赫曼原理推广应用于复摆振动问题，即“其作用下的推动力应当是构成摆的重物，为使有可能一起运动，这些推动力等价于在重力作用下所得到的那些力；因此，如果它们的方向相反，则前者与后者应处于平衡”这个原理是拉格朗日形式的达朗伯普遍原理的前奏。

在此期间欧拉还研究了等周问题，即在给定长度的所有简单闭曲线中确定一条线使之保持最大面积的问题，并发表了一系列文章，这些文章奠定了数学新领域－变分学的基础。1744年欧拉发表了变分学着名论文，其中特别给出了定积分

取极值的必要条件。

为了导出上述条件，欧拉将区间［a，b］分成代横坐标x₀=a，x₁，x₂，…，x_n，x_n+1=b的相等小区间，用代纵坐标y_s=f(x_s)的折线代替未知曲线y=f(x)，用有限差之比f′(x_s=(y_s+1－y_s)／(x_s+1－x_s)代替导数，用有限和

代替积分(2)。

为了确定函数S′的极值，取其对y_s+1的导数并让它等于零，得到方程

且Δx=x_s+1－x_s．在ΔS→0的极限下，得到欧拉方程

我们简略地叙述谢道夫(Ceдов)变分方程，它是基于变分方法对不可逆过程的推广。

谢道夫方程有形式

其中V为连续介质的任意体积，［t₀，t₁］为任意时间间隔，［(1／2)v_ivⁱ－U］为拉格朗日函数，δW^*和δW是如下形式的泛函：

并且ρ为质量密度，U和S为单位质量的内能密度和熵密度，xⁱ为坐标，vⁱ=dxⁱ／dt为速度，T为温度，δG′为非补偿热，和分别为外体力和面力的功。

在方程(3)中，拉格朗日函数A和泛函δW^*是给定量，泛函δW由方程(3)确定，它的计算相应于建立状态方程。

变分方程(3)实际上是考虑到热力学第一、第二定律所描述的连续介质的动力学普遍方程对时间的积分。

变分方程(3)由谢道夫(1965)给出，与建立复杂性质连续介质新模型的问题相关。

谢道夫将这个变分方程作为连续介质力学的原始公设。在变分方法范围内建立新的模型，包括确定选取等定函数并给出拉格朗日函数A和泛函δW^*。

高斯(Gauss 1829)赋予达朗伯一拉格朗日原理以极值原理的形式。引入仅在加速度上不同于真实运动的想象速度，高斯证明了对于真实运动来说，拘束有极小：

赫兹(1894)在建立无力力学时提出了直路(或最小曲率)原理

它实际上是特殊情形F_v=0时的高斯原理。

契塔耶夫(1941)给出了高斯原理的变形，证明了对于真实运动来说，如果力学系统是完全自由的，那么由在作用力场中高斯的正向想象运动和为建立真实运动所需力场中的倒退(反向)运动两者组成的基本循环上的功A是极大：

其中为想象运动中的加速度。

注意到这个原理是赫曼和欧拉思想的直接变形，拉格朗日在叙述达朗伯原理时发展了这个思想，运用热力学卡诺(Carnot)原理的办法，契塔耶夫原理可扩充通常研究的力学系统的特性。

这个原理在物理系统方面的推广形式有

其中U为内能，ΔQ为热流，并利用热力学第一、第二定律。这就是物理系统的契塔耶夫原理。

最后我们简述最优控制的最简单问题，这个问题是在问题

中，在条件

x(t₀)=x₀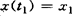，，u(t)∈U

下，来寻求必要条件。

设可允控制类由代第一间断点、在某闭域U上取值的所有分段连续有界函数u(t)组成。这个问题就是庞特里雅金(ЛонTpягин)提法下变分学的拉格朗日问题，类似问题的本质特征是事先确定在闭域U上取值的可允控制类。

如果在研究中引入庞特里雅金函数

那么，相变量xⁱ和起拉格朗日乘子作用的辅助变量φ_i的方程可写成正则形式

(i=0，1，…，n)

下述定理成立：设u(t)，t₀≤t≤t₁是相点由位置x₀到位置x₁过渡的可允控制，而x(t)是相应的轨道，于是x(t₀)=x₀，x(t₁)=x1(时刻t₀，t₁固定)。为使u(t)给出代固定时间的最优问题的解，必须存在与u(t)和x(t)对应的、非零连续矢量函数ψ(t)=(ψ₀(t)，ψ₁(t)，…，ψ_n(t))，使得

①对所有t，t₀≤t≤t₁，变量u∈U的函数П(ψ(t)，x(t)，t，u)在点u=u(t)达到极大

②函数ψ₀(t)=const为非正。

显然，庞特里雅金极大值原理属于微分变分原理范畴。

当控制的可允值集合为开集时，极大值原理等于着名的维尔斯特拉(Weierstrass)条件。但在控制落到域U的边界上时，维尔斯特拉条件一般说不满足，而极大值原理此时也是对的。

可以证明，最优原理也可表为积分变分原理形式

在一般情形下，由这个积分原理可导出运动方程，边界条件和横截性方程以及庞特里雅金极大原理。

(合肥工业大学朱永春撰)