线性支出系统
出处：按学科分类—经济 经济科学出版社《消费经济学大辞典》第171页（2929字）
在S·R·斯通(Sir Richard Stone)的开创性工作之前，计量经济学家对消费者需求——支出关系进行经验研究时，很少涉及到理论经济学家对消费者最优选择行为的分析，二者缺乏沟通。
斯通的线性支出系统模型是较早将理论分析与经验研究完美结合的典范，它的计量模型有很好的理论根据。
L·R·克莱因(L．R．Klein)和H·鲁宾(H．Rubin)于1947年提出了如下形式的效用函数：
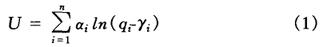
其定义域是qi＞γi＞0，i=1，2，……，n。
qi是商品i的实际需求量；γi可解释为维持生活的基本需求量；αi为加权参数，满足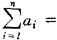
1。
(L．R．Klein and H．Rubin，A Constant Utility Index of Cost of Living，Review of Economic Studies，vol．18(1949－50)，pp．65－66．)
1954年斯通假定消费者以(1)式为效用最大化目标，在支出预算约束：
其中pi代表商品价格。
下求得LES需求支出函数：
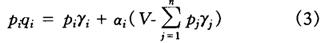
i=1，2，……，n，V是总支出。(参见R．Stone，Linear Expenditure System and Demand Analysis：An Application to the Pattern of British Demand，Economic Journal，vol．64(1954)，pp．511－527)
(3)式表明，LES模型有明确的经济解释：消费者对商品i的需求支出额可分为两部分之和，第一部分为该商品的基本需求支出piγi；第二部分是总预算支出V减去对所有商品的基本需求支出后剩余部分中用于商品i的部分，其份额是αi。
V、pi为外生变量，qi为内生变量，αi、γi为待估计的参数。LES假定基本需求支出不随预算V的变化而变化，边际预算份额αi对所研究的消费者都相同，也与V的变化无关。
由(3)式得需求函数
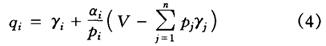
商品i的总支出弹性为：
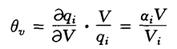
其中Vi=piqi。自价格弹性为
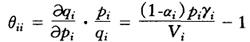
互价格弹性为
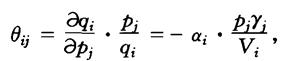
其中j=1，2，…，n，j≠i，且满足需求函数应有的性质：
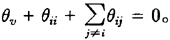
若以价值量为需求单位，由(3)式可得需求的总支出弹性为：
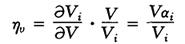
自价格弹性为
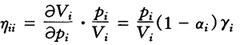
互价格弹性为
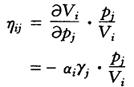
其中j=1，2，…，n，j≠i，但有下式成立：
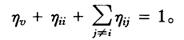
LES模型有一个理论逻辑不足：即假定总支出V为外生，这是不妥的，消费者通常的行为不是先确定总支出再购买商品，即总支出决定商品购买，而是购买决定了总支出。
1973年陆驰(Liuch)用收入I替代LES模型中的V，提出了扩展线性支出系统(ELES：Extended Linear Expenditure System)的需求函数：
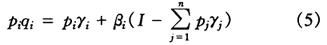
i=1，2，…，n，参数βi是边际消费倾向而非边际预算份额，满足：
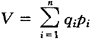不再是外生变量，而由消费者购买行为内生地确定。
ELES(或LES)的估计方法。
ELES模型中需要估计的参数有βi和piγi(i=1，2，…，n，如果知道价格，可求商品的基本需求量，因商品类的价格不易得到，常以价值量为需求单位)，它们是非线性的待估参数。参数估计方法有很多，比较简单、使用的方法有最小二乘法和迭代法。
最小二乘法 将模型(5)写为计量形式：
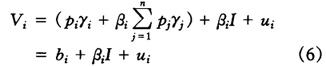
ui为随机扰动项。对(6)式应用最小二乘法(对于截面样本数据，可能存在异方差性，宜用加权最小二乘法WLS)，得到参数估计值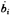
和
=1，2，…，n)。
因为
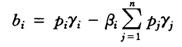
得
从而
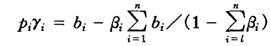
再由bi和βi(i=1，2，…，n)可求得piγi的估计值。如果是截面样本数据，商品类的价格不随收入的变化而变化，可求出基本需求量γi，但因价格不变而不能计算商品需求的价格弹性。
迭代法 迭代法是非线性参数计量估计的常用方法。将(5)式中的参数分开，模型变为两种形式，每一种形式只含一组待估参数且为线性形式，可用普通最小二乘法(OLS)估计。利用在模型的两种形式之间相互迭代，直至参数估计值达到收敛。
具体步骤如下：
设Yi=Vi－βiI
Xi=(－βip1，…，－βipi－1，(1－βi)pi，－βipi+1，…，－βipi)
R=(γ1，γ2，…γn)′
U=(u1，u2，…，un)′
样本回归模型可写成
Y=XR+U (6)
其中
Y=(Y1，Y2，…Yn)′
X=(X1，X2，…Xn)′
再设
Wi=Vi－piγi
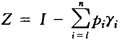
B=(β1，β2，…，βn)′
则模型又可写为
W=Z·B+U (7)
其中
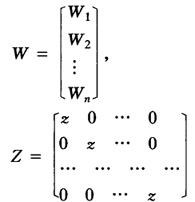
先给定βi(或γi)的初始值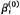
(或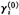
)，利用OLS法由(6)式(或(7))可估计得到参数
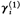(或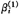
)，然后将它们代入W和Z(或X和Y)，利用(7)式(或(6))求得βi(或γi)的估计值
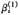(或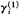
)，…反复迭代，直到两次迭代中得到的参数估计值满足收敛条件为止。迭代法要求商品类的价格pi为已知。