等精度观测值的平差
出处:按学科分类—工业技术 中国建材工业出版社《工程测量实用技术手册》第98页(1783字)
平差是对一系列观测值采用适当而合理的方法,消除或减弱其误差,求得未知量的最可靠值,并评定测量成果的精度。通常我们把求得的未知量的最可靠的值,称为最或然值,它十分接近于未知量的真值。
1.求未知量的最或然值
设对某未知量进行了n次等精度观测,其真值为X,观测值为l1,l2,…,ln,相应的真误差为,△1,△2…,△n,则
△1=l1-X
△2=l2-X
…
△n=ln-X
将上式取和再除以观测次数n便得

式中x为算术平均值,显然 。
。
根据偶然误差第四个特征,当n→∞时, ,因此
,因此

即当观测次数n无限多时,算术平均值x就趋向于未知量的真值X。当观测次数有限时,可以认为算术平均值是根据已有的观测数据所能求得的最接近真值的近似值,称为最或是值或最或然值,以它作为未知量的最后结果。
2.等精度观测值的评定精度
(1)观测值的似真误差
根据中误差定义式计算观测值中误差的m,需要知道观测值li的真误差△i,但是真误差往往不知道。因此,在实际工作中多采用观测值的似真误差或改正数来计算观测值的中误差。用vi(i=1,2,…,n)表示观测值的似真误差,或称观测值的最或然误差,而改正数则与误差符号相反。
v1=l1-x
v2=l2-x
…
vn=ln-x
等式两端分别取和
[v]=[l]-nx
因为 ,所以[v]=0
,所以[v]=0
即观测值的似真误差代数和等于零。上式可作为计算中的校核,当[v]=0时,说明算术平均值及似真误差计算无误。
(2)用似真误差计算等精度观测值的中误差
计算公式为
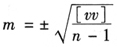
上式推导如下:
△i=li-X
vi=li-x
以上两个等式相减得:
△i-vi=x-X
令δ=x-X,代入上式并移项后得
△i=vi+δ
以上n个等式两端分别自乘得
△i△i=vivi+2viδ+δ2
上式有n个取和得
[△△]=[vv]+2δ[v]+nδ2
因为
[v]=0
所以
[△△]=[vv]+nδ2
等式两端分别除以n得


上式平方得

由于△1,△2,…,△n为偶然误差,故非自乘的两个偶然误差之积△1△2,△1△3…仍然具有偶然误差性质,根据偶然误差的第四个特性,当n→∞时,上式等号右端的第二项趋于零。因此得



顾及中误差公式,上式可写为

3.等精度双观测值的较差计算中误差
在边长观测中,一般采用往返观测,因此出现等精度双观测列,例如

相应双观测列之差:

如果观测是绝对正确的,那么每个差d都等于0,即d的真值为0。因此,d1,d2,…,dn可以认为是各差的真误差。按真差求中误差得

根据前文介绍可知,两等精度观测值之差d的中误差为一个观测值中误差m的 倍,故
倍,故
