常用几何图形的面积和体积的计算公式
出处:按学科分类—工业技术 华南理工大学出版社《建筑工程造价计算手册》第4页(7233字)
(1)梯形

式中 a、b-上底长和下底长;
h-高;
S-面积(以下同)。

(2)菱形

式中 D-长对角线长;
d-短对角线长。

(3)正多边形

式中 n-边数;a-边长
r-边心距;
α-2π/边数;
R-外接圆半径。

(4)圆

式中 D-直径;
r-半径。

(5)圆环
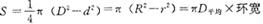
式中 D-外圆直径;
d-内圆直径;
R-外圆半径;
r-内圆半径。

(6)扇形

式中 L-弧长;
r-半径;
a-圆心角。

(7)缺圆环

式中 R-外半径;r-内半径;a-中心角。

(8)弓形


式中 L-弧长;r-半径;a-圆心角;h-突起;a-弦长。

(9)椭圆
S=πab
式中 a-长半轴;
b-短半轴。

(10)椭圆环
S=π(ab-a1b1)
式中 a-外椭圆长半径;
a1-内椭圆长半径;
b-外椭凹短半轴;
b1-内椭圆短半轴。

(11)抛物线

式中 b-宽;
h-高。

(12)正立方体
V=a3
式中 V-体积
(以下同);
a-边长。

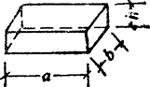
(13)长立方体
V=abh
式中 a-长;
b-宽;
h-高。
(14)多角柱体
V=Sh
式中 h-高
S-底面积

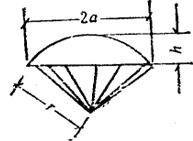
(15)六角锥体

式中 h-高;
S-底面积。

(16)三棱柱体

式中 a、b、c-分别为
三棱柱体的三个边长;
S-三棱柱断面积。

(17)棱台

式中 S及S0-分别为上下底面积;
a、b-边长;
h-高。

(18)楔形体(两侧为等腰三角,前后为梯形)


(19)圆柱
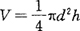
S侧=πdh
式中 d-直径;
h-柱高。

(20)斜切正圆柱

S侧=πr(h1+h2)
式中 h及h1-分别为斜切正圆柱的高;
r-半径。

(21)中空圆柱

式中 h-高;
D及d-分别为外内直径。

(22)球

S=4πr2
式中 r-球半径

(23)球锥体(球楔)

S全=πr(2h+a)
式中 h-突起;
a-弦长的一半;
r-半径。
(24)弓形体(缺圆)

S侧=2πrh(不包括底面积)
式中 h-突起;
a-弦长的一半;
r-半径。

(25)球截体(球带体)

S侧=2πrh

式中 r-半径;
h-拱高。

(26)圆截面环(圆环体)
V=π2·Dr2
S=4π2Rr=π2Dd
式中 R-环体半径;
D-环体直径;
r-环体断面半径;
d-环体断面直径。

(27)正圆锥体

式中 r-底半径;
h-高;
l-母线长。

(28)平截正圆锥体

S侧=πl(R+r)
式中 r-上底半径;
R-下底半径;
h-高;
l-母线长。
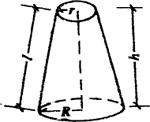
(29)平裁空心圆锥体

式中 D1及D2-分别为下底外直径和内直径;
d1及d2-分别为上底外直径和内直径;
δ-圆锥体厚度。

(30)正圆体的斜劈


(31)桶状体


式中 D-桶腹直径;d-桶底直径;h-桶高。

(32)椭圆体

(绕a-a轴旋转时)

(绕b-b轴旋转时)
式中 a、b、c-分别为椭圆体三个方向的半径

(33)正四面体
棱:6
顶点:4
S=1.7321a2
V=0.1179a3
a=棱长

(四个三角形)
(34)正八面体
棱:12
顶点:6
S=3.4641a2
V=0.4714a3
(八个三角形)
(35)抛物线体

式中 D-直径;
R-半径;
h-高;
V-体积。

(36)交叉圆柱体

式中 r-圆柱半径;
L、L′-圆柱的长;
V-体积。

(37)直通式砖格子的用砖数

式中 N-每层砖格子所用格子砖块数;
F-砖格子室的横断面积(mm2);
S-格孔尺寸(mm);
d-格子砖的厚度(mm)。
