可靠性设计的基本原理
出处:按学科分类—工业技术 企业管理出版社《工程师手册》第276页(5093字)
定量描述可靠性的定义,是从五十年代初期开始的。随着科学技术的发展,对所研究和考虑的问题已走向了系统的时代。系统越来越复杂,因而也越容易发生故障,使系统失效。在工程设计中,为了提高系统的性能,只好提高对元件的要求。例如,各元件的可靠度相等,都为99.9%,那么,40个元件串联的系统,其可靠度约为99%,由400个元件串联的系统,可靠度就下降为60%;如果系统中有30万个元件,为了保证系统能达到90%的可靠度,则每个元件的可靠度就要达到99.9999%,这样,系统的造价就很昂贵,甚至难以实现。如何从设计解决系统的可靠性,改善对每个元件的可靠度的要求,这就是可靠性设计所要解决的问题。因此,概括地说,可靠性设计就是往事前考虑系统可靠性的一种设计方法。
可靠性设计,必须全面考虑(包括从研究试制到使用和维修)产品的寿命周期。虽然系统的复杂程度、类别、可修复与不可修复、工业产品与民用产品、研制产品与定型产品等的不同,以及可靠性设计方法和重要程度的不同,但其设计原理则大体上是一致的,其核心就是可靠度的分配。
可靠度分配,就是为了改进某系统、设备的可靠度,或重新设定设计指标时,如何将已知系统的可靠度分配给其组成部分的过程。采用可靠度分配的优点是:(1)当功能、重量和费用相同时,作为系统参数,可靠度能以明确的形式来表示;(2)通过设计、制造和试验等过程,不仅可保证系统可靠度,而且还可不断提高可靠性技术水平:(3)通过掌握系统、子系统、组件和零件等的关系,能明确设计方面的基本问题,(4)可靠度的值较分配前更切合实际;(5)与满足现定可靠度相比,可节约时间和费用。此外,最佳系统的可靠度,应在考虑对一般组成可靠度部分的系统的重要度、工作周期、目前的技术水平、功能的完成度等之后,再作决定。
分配的原则有:(1)必须考虑系统所要求的可靠度;(2)组成部分的技术等级,即从可靠性难度来衡量的等级;(3)必须考虑到系统与组成部分可靠性的关系;(4)在系统工作时间内,组成部分的动作时间;(5)组成部分可靠度对系统可靠度所起的作用;(6)应通过分配来改进系统可靠度;(7)必须考虑系统的功能、性能、成本与时间的平衡和费用有效性等;(8)最好分配单元的可靠度随技术水平的提高而提高;(9)单元对系统的重要度愈增加,就愈要提高组件的可靠度;(10)即使增加工作周期或动作时间,分配组件的可靠度也不应发生变化(即动作时间增加,分配的故障率会减小);(11)在相同系统中的部件,无论是串联系统还是冗余系统,当具有相同的重要度、工作周期和技术等级时,应具有相等的分配可靠度。此外,还要考虑研制的费用、时间、技术的难易、故障相对频率、单元的复杂性和环境条件等。
可靠度的分配方法有如下几种:
(1)简单可靠度分配数值法。在决定可靠度分配时,首先要明确设备和系统的整体与其组件间的性能关系,并在此基础上把系统可靠度分配给各组成部件。最常用的是串联模型。如果有n个相同的单元组成串联系统,系统的可靠度为R,其部件的可靠度为R1,则
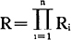
例如,有三台重要程度相同的仪器等效串联排列,当系统的可靠度要求为0.9时,各仪器的可靠度则为
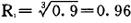
假定其中一台仪器的可靠度为R1=0.99时,则其余两台仪器的可靠度则为
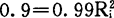 ,R1=0.956,i=1.2
,R1=0.956,i=1.2
如果以上不是指可靠度,而是有效度A,只需将Ri的积换成A1的积即可。
(2)按相对故障率分配可靠度。当系统为串联时,设系统和单元的可靠度是故障率,规律为指数分布;而单元相互独立。若系统工作时间为T,构成单元i的工作时间则为t1(0<t1≤T)。现设系统是由n个单元串联组成,其故障率分别是λ1、λ2、…λn,从数据预测的故障率为λ1、λ2、…λn,则全系统要求的故障率λ为 ,其重要度W1可用下式表示:
,其重要度W1可用下式表示:
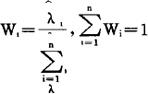
由上式可得,分配到单元的故障率为
λi=w1λ
将此关系代入可靠度,则因所要求的系统可靠度R(t)为
R(t)≤e-(∑λ1)t=e-(Σwi)λt=e-λ1
故分配到单元的可靠度为
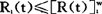
反之,如果给出的不是故障率,而是系统所要求的可靠度R(T),那么,系统所要求的故障率λ为
λ=[-InR(T)]/T*
分配到单元的可靠度Ri(t)为
R1(t)=e-λ1T
(3)按重要度分配可靠度。无论串联或并联系统,当已知各组成部分的重要性时,可按其重要度分配可靠度。所谓重要度,是指组成部分的故障率与系统故障率或相对故障率之比。如按单元故障把系统发生故障的概率定为Ei,则不可靠度F1≈λit1,在串联系统中
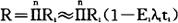
如n个单元的可靠度都相等,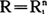 ,则可按下式来分配故障率:
,则可按下式来分配故障率:
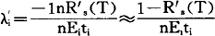
从上式可知,如E1、t1、n、R′s愈大,λ′i的分配就应愈小。其中R′i;为目标系统的可靠度,分配时系统可靠度应高于目标系统的可靠度,即
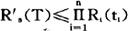
当串联单元中所含的重要零组件的相对比率为n1/n(n=∑n1)时,则
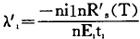
如果各单元的重要零件n1很少,相对地使组件变得简单,就易于获得高可靠度。因而,如按上式分配,则Ei、t1、R′s愈大,或n1/n愈小,λ′1就分配得愈小。例如,由5个单元构成的串联系统,其单元的复杂性以晶体管的数目而定,其值分别为35、91、88、231和88;工作时间t1=t2=t3=t4=12小时,t5=6小时;E1=E2=E3=E4=1.0,E5=0.25;系统所要求的可靠度为0.9。则n=533,按上述公式可求得分配组件的故障率为:
λ′1=-{35Xln0.9}/(533×1×12)=575×10-6小时。同样,λ2、λ3、…λ5如以10-6/小时为单位,则分别为1495,1445,3790,11560。
(4)按综合指标分配可靠度。作为分配的重点,在单元和子系统中算出现在的技术水平In,环境应力指数If,整个系统的工作时间对组件的工作时间之比Im,以及组件的复杂性(零部件数和冗余数)指数Ik等,并求出综合指数I1=In(Ik+If+Im),然后根据其相对比值Ei=I1/(∑Ii),按重要程度分配,即
R′i=REi=(1-F)E1≈(1-E1F)
例如,由四个单元构成的串联系统,其预测的每个单元的失效率分别为0.003、0.002、0.004和0.007(1/小时),所要求的系统故障率λ=0.01/小时。因为∑λi=0.016,由此可得相对比率W1,并经乘以0.01后,所分配的单元失效率λ1则分别为0.001875,0.00125,0.0025,0.00437。当t=10小时时,因为R(10)=e-0.01×10≈0.9,可求得单元的可靠度分别为0.98,0.978,0.974,0.955。
(5)按复杂性(故障率)和重要系数分配可靠度。组件的系统重要度Wi愈大,故障率就愈小,分配的故障率也愈小。决定这种分配比例的分配系数Ki,可用复杂性Ci(如零部件数)表示为
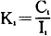
如果零部件数不明确,也可以故障率λ1取代C1。这里的Ii是影响度,它与Wi不同,象并联系统的设备一样,如故障不立即导致全系统发生故障时,选择I1=1。因此,Ii可以用因设备故障引起系统发生故障的概率P1(失效率)求得,即
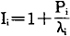
但由于并联系统的P1=0,故应分得的K的比值就是故障率的比值。
对于串联系统,如以λ′作为系统故障率,则分配单元的故障率λ′1为
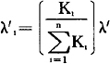
并联系统的可靠度服从指数分布,由于在高可靠度的范围内,根据R=e-λt≈1-λt,F=λt,所以,如设系统的故障率为λs,工作时间为T,单元的故障率为λi,工作时间为ti,则n个单元并联时
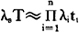
如设T=t1=t,则
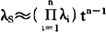
假定是两个单元并联,则λs=λ1λ2t。因Ei=0,Ii=1,所以分配系数为
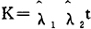
当以复杂性Ci代替λi时,可认为λi与C1成正比,即
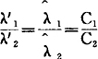
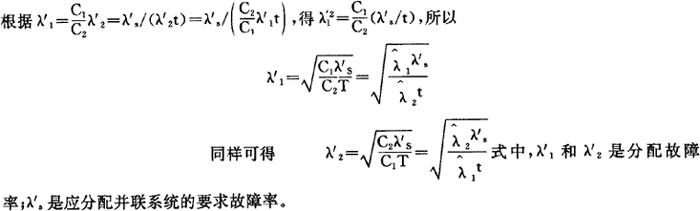
图2.4.4-1是一串并联系统,当t=500小时,要求的可靠度为99%。各单元的故障率及由于单元故障引起系统故障率如表2.4.4-1。首先,求出R=0.99、t=500小时的要求故障率λ=20×10-6,其次求出各单元的分配系数K,见表2.4.4-2。这里,先求出并联部分的分配系数,然后求出与A、C串联的全系统的分配系数K。因为EB串联部分的故障率为9.0×10-6/小时,D的故障率为10×10-6/小时,则并联部分的分配系数为
表2.4.4-1

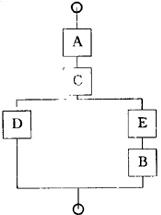
图2.4.4-1 串并联系统
表2.4.4-2

K并=λ1λ2t=90×10-12×500=4.5×10-8
因K1在单元A为1×10-6,在单元C为9.1×10-6,在并联部分K并=4.5×10-8,因而
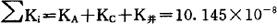
由此,分配的故障率为
λA=20×10-6×1/10.145=1.97×10-6(1/小时)
λc=20×10-6×9.1/10.145=17.94×10-6(1/小时)
λ并=20×10-6×4.5×10-2/10.145=8.88×10-8(1/小时)
然后把λ并分配给各单元:
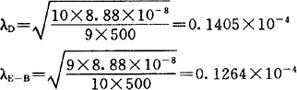
最后再把λE-B分成成E和B,即
λE=0.1264×10-4×1/(1+6.53)=0.0168×10-4
λB=0.1264×10-4×6.53/(1+6.53)=0.1096×10-4