风险型决策
出处:按学科分类—工业技术 企业管理出版社《工程师手册》第445页(2811字)
风险型决策也叫概率型决策,这类决策的主要特征是:决策的问题存在两种以上的自然状态,且决策者对其无法控制;今后出现哪些自然状态,决策者不能肯定,但其出现的概率,决策者可依据历史统计资料和经验推断,大致地估算出来。但这种概率估计往往还有一定的主观因素,因而这类决策存在一定的风险性。风险型决策主要应用于远期目标的战略决策,或随机因素较多的非常规型决策,诸如企业投资决策、新产品开发决策、技术改造决策和市场营销决策等等。那么,对这类问题依据哪些准则或方法进行决策呢?
1.最大期望收益值准则
期望值,是指某方案的实施期望可获得的损益值。某一方案的期望值等于其在各自然状态下的概率乘以该方案在此状态下损益值的总和。其数学表达式为:
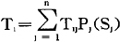
式中:Ti——第i方案的期望值;
Tij——第i方案在自然状态Sj下的损益值;
Pj(Sj)——自然状态Sj的概率;
Sj——为每一方案可能遇到或发生的状态。
决策时,首先要计算出每个方案的期望损益值,然后按一定准则决策选优。“最大期望收益值”准则,是指从收益角度出发,从各方案中选择最大期望收益值的方案为最优方案(Ta)的决策准则。其数学表达式为:
Ta=max{T1,T2,……Tm}
2.比较优势准则
比较优势准则,应用于很多方案的初选决策,即从众多方案中选择出几个较有优势的方案的初选决策,而不是选择一个最优方案的最终决策。具体地说,通过诸多方案损益值的对比,确定某些方案为优势方案,则予以保留;某些方案为劣势方案,则舍弃之,从而减少最终决策的备选方案数目。
3.最小期望机会损失值准则
最小期望机会损失值准则就是选择期望机会损失值最小的方案为最优方案的决策准则。
4.决策树技术
风险型决策除了以决策收益表为基础,根据不同情况分别以上述相应的决策原则进行决策外,还可以用决策树进行决策。决策树不仅可以解决决策收益表表达的单阶段决策问题,而且还可以解决收益表难以表达的多阶段的序列决策问题。
(1)决策树的结构
决策树是以方块和圆圈为结点,并由直线把它们连结起来的形似树状的结构,如图2.6-1所示。图2.6-1中,方块结点表示决策事件符号,称决策点;由决策点引出若干条树枝,每条树枝代表一个方案,称之为方案枝;圆圈结点是概率点,由概率点引出若干条树枝,每条树枝表示一种自然状态,称其为概率枝;在概率枝末端列出该自然状态下的损益值。由于决策的问题是多方案的,且每一方案又可能有多种自然状态,因此,图形由左到右,由简到繁构成一个树枝网状结构图。
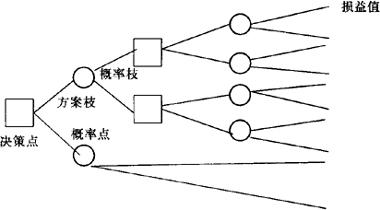
图2.6-1 决策树结构
(2)决策的步骤
第一,绘制决策树图形。决策树是人们对某个决策问题未来发生情况的可能性和可能结果所作预测在图纸上的反映。所以,绘制决策树的过程,就是拟定各种备选方案的过程,也是对所要决策问题未来可能发生的各种事件步步深入推进的过程。图形绘制由左向右进行。
第二,计算期望值。从右至左,算出各概率点的损益期望值,即将每种自然状态下的收益值乘各自的概率,它们的总和就是该方案的期望值,并将其标在相应概率点上方。
第三,修枝选优。根据不同方案期望值的大小,从右向左逐步后退进行修枝选优。期望值大的为最优方案,期望值小的方案予以舍弃,即在方案枝上画“×”符号,最后在决策结点上只留下一条树枝,它所代表的就是最优方案,并将最优方案的损益期望值标在决策点上方。
(3)单阶段决策实例分析
某企业要在生命周期为五年的A、B、C三种专利产品中选择某一种投入生产,所需投资总额(包括固定资产、流动资金和专利费用)分别为250万元、155万元和72万元。该三种专利产品在市场景气、一般、不景气三种自然状态下的销售概率分别为0.3、0.5和0.2;且据测算若五年内全部回收投资后,A产品在一种自然状态下可获利润350万元、150万元、-200万元,B产品为250万元、125万元、-125万元,C产品为100万元、50万元和-25万元。现企业选择何种专利产品投产,其年均期望投资报酬率最高?
首先,绘制决策树图形,并将有关数据标在图上,以便分析。决策树图如图2.6-2所示:
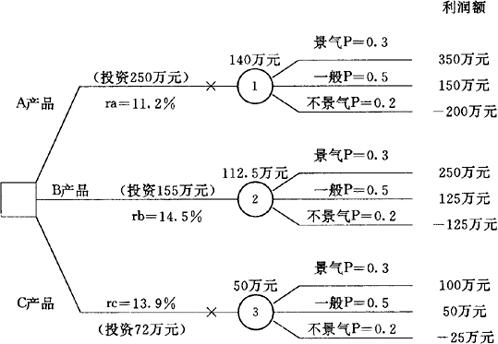
图2.6-2
其次,从右向左分别计算各方案五年内的期望利润,并标在相应的概率点上。
概率点①:350×0.3+150×0.5+(-200)×0.2=140万元
概率点②:250×0.3+125×0.5+(-125×0.2)=112.5万元
概率点③:100×0.3+50×0.5+(-25×0.2)=50万元
再次,计算各方案的投资年均期望利润率,并修枝选优。
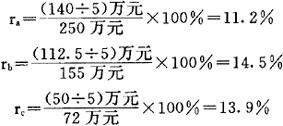
这表明A、B、C三种专利产品投产五年期间,其年均投资报酬率分别为11.2%、14.5%和13.9%,由于rb>rc>ra,所以选择专利产品B投产为最优方案。
(4)多阶段决策
若决策问题较复杂,则要创建阶段决策。应用决策树技术于多阶段决策,较为清晰明了。