纯整数规划(IP)模型

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第684页（922字）

整数规划用于含离散型变量的决策问题。由于项目及项目中某些与生产能力有关的装置具有不可分性的特点，使得表示项目取舍及某些装置投入运营的台套数的决策变量只能取整数。因此，整数规划在项目群优化选择中得到广泛的应用。

整数规划中如果所有的变量都是整数型，称为纯整数规划。纯整数规划的一种重要形式是0－1整数规划，0－1整数规划中决策变量的取值只能是0或者1。如果项目群中各个项目方案的费用和收益是彼此独立的，即每一个项目一旦投入运营，其投入产出情况与其他项目无关，因而其费用和收益可以在决策前独立确定，不取决于其他项目最终选取与否，则对于任何一个项目方案来说，选择结论只有两种可能：或者被接受，或者被拒绝。在这种情况下，就可以为项目群优化选择建立0－1整数规划模型。通常，当接受一个项目方案时，令其决策变量值为1；拒绝一个项目方案时，令其决策变量值为0。

0－1整数规划模型的一般形式为

目标函数MaxZ=∑C_j·X₁(净现值总和最大)

或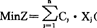(总费用现值最小)

约束方程∑a_ijXj≤(=，≥)b₁

i=1，2，…，m；j=1，2，…，n

式中，X_j为第j个项目方案的决策变量，Xj的取值为1或0。C_J、b_J、a_IJ均为已知模型参数，通常C_j表示第j个项目方案的净现值或费用现值；b_J表示第i种资源约束或其他约束的限界值；a_IJ表示第j个项目方案耗费第i种资源的数量或反映与其他约束条件的关系。

0－1整数规划用于项目群选优，其原理与互斥方案组合法是完全相同的，都是从可行的组合方案中选取经济效果最好的组合方案。但二者在对问题的描述方式和解算效率上有明显差别。通过对比分析说明0－1整数规划方法与互斥方案组合法的异同。