随机变量
出处:按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第65页(1873字)
若对每次实验结果,可用一个数ξ来表示,且对任何实数x,ξ<x有确定概率,则称ξ为随机变量。而称
F(x)=P(ξ<x) (2.2-2)
为ξ的分布函数。
我们经常遇到两种随机变量:
1.离散型:ξ取值x1,x2,……可列,且有确定概率
P(ξ=xi)=pi
2.连续型:ξ存在分布密度(简称密度)f(x)≥0使
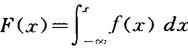
为说明随机变量ξ分布的性质,我们要用到分布的数字特征:
期望

方差
V(ξ)=E{(ξ-E(ξ))2} (2.2-4)
期望亦称均值,为平均值概念的推广。方差的正平方根即标准差

此外还用到
k阶原点矩 αk=E(ξk)
h阶中心矩 μk=E{(ξ-E(ξ))k}
〔例2.2-1〕 对称两点分布

图2.2-1 对称两点分布
此分布仅在-c,+c两点取值,且
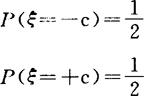
其期望与方差由离散型算法为
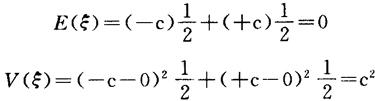
〔例2.2-2〕 正态分布
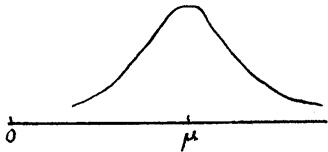
图2.2-2 正态分布
连续型随机变量ξ服从正态分布指其

记为ξ~N(μ,σ)且以后‘~’均表服从。其期望与方差由连续型算法为
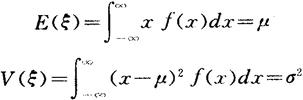
故N(μ,σ)括号中两参数为期望与标准差。
正态分布亦称高斯分布。
〔例2.2-3〕 均匀分布

图2.2-3 均匀分布
连续型随机变量ξ服从均匀分布指其
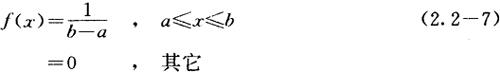
记为ξ~U〔a,b〕。其期望与方差为

【参考文献】:
[1]王立吉,计量学基础,中国计量出版社,1988。
[2]BIPM、IEC、IFCC,IUPAC,IUPAP,OIML,Guide to the Expression of Uncertainty in Measurement, ISO,1993.
[3]刘智敏,不确定度原理,中国计量出版社,1993。
[4]刘智敏,误差分布论,原子能出版社,1988。
[5]刘智敏,误差与数据处理,原子能出版社,1983。
[6]Liu Zhimin(刘智敏),Measurement Uncertainty and Its Correlation Combination,Proceeding of ISEM, 1993.
[7]国家计量总局量值传递处编,计量技术考核纲要,计量出版社,1981。
[8]国家技术监督局审定,刘智敏等编审,全国计量检定人员考核统一试题集第六分册三,误差及数据处理,陕西科学技术出版社,1990。