确定合成标准不确定度与展伸不确定度
出处:按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第102页(2080字)
1.合成标准不确定度
由
y=f(x1,x2,…xN)
知合成标准不确定度uc(y)的平方

式中r为相关系数。
引入不确定度分量

如各r(xi,xj)=0,则

即各分量无关时,用平方和法合成。
如各r(xi,xj)=1,且 符号相同,则
符号相同,则
uc=∑ui (2.6-14)
即各分量完全正相关,用线性和法合成。
uc(y)可简写为uc。
如有u1=1.0,u2=1.0,u3=1.0,当无关时 ,当完全正相关时uc=∑ui=3.0
,当完全正相关时uc=∑ui=3.0
2.展伸不确定度
(1)t分布应用
对某量作等精度独立测量,得
q1,q2,…qn
则该量最佳值为

其估计标准差
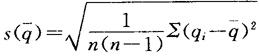
如qi~N(μ,σ),我们有

而自由度v=n-1。
因t分布临界值tp(v)满足
P(|t|≤tp(v))=p
故以置信水准p成立
 (2.6-15)
(2.6-15)
 (2.6-16)
(2.6-16)
而
 (2.6-17)
(2.6-17)
〔例2.6-6〕 测得的qi如下
1011.46 1010.76
1011.01 1014.13
1012.29 1012.98
1013.47 1010.46
1014.07 1011.25
1010.60 1012.02
于是

取置信水准p=0.95,由表2.2-1查得tp(v)=t0.95(11)=2.20,故

(2)确定展伸不确定度
虽然uc(y)可通用于表示测量结果不确定度,但在某些商业、工业及规程中,当涉及健康,安全等因素时,还须将uc(y)放大,以得到展伸不确定度
U=kuc(y) (2.6-18)
式中k为包含因子。而
k=tp(v) (2.6-19)
为t分布临界值,且p为置信水准,又合成标准不确定度自由度

而vi为ui的自由度。
当缺乏vi时,则v无法算出,此时取
k=2-3
【参考文献】:
[1]王立吉,计量学基础,中国计量出版社,1988。
[2]BIPM、IEC、IFCC,IUPAC,IUPAP,OIML,Guide to the Expression of Uncertainty in Measurement, ISO,1993.
[3]刘智敏,不确定度原理,中国计量出版社,1993。
[4]刘智敏,误差分布论,原子能出版社,1988。
[5]刘智敏,误差与数据处理,原子能出版社,1983。
[6]Liu Zhimin(刘智敏),Measurement Uncertainty and Its Correlation Combination,Proceeding of ISEM, 1993.
[7]国家计量总局量值传递处编,计量技术考核纲要,计量出版社,1981。
[8]国家技术监督局审定,刘智敏等编审,全国计量检定人员考核统一试题集第六分册三,误差及数据处理,陕西科学技术出版社,1990。