标准不确定度的A类评定
出处:按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第98页(2304字)
1.一个量的等精度独立测量
当对一个待求量Xi作等精度独立测量,得
xi1,xi2,…,xini
则最佳值

按2、4、3,xi的标准差即A类评定的标准不确定度可按以下算出
(1)贝塞尔法
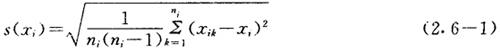
其自由度因 有一个限制条件∑(xik-xi)=0而为
有一个限制条件∑(xik-xi)=0而为
vi=ni-1
(2)彼得斯法、极差法、最大误差法、最大残差法
彼得斯法

极差法

最大误差法

式中xi0为xi的真值。
最大残差法

极差法所用系数见表2.4-1,最大误差法所用系数见表2.4-2,最大残差法所用系数见表2.4-3。
由算s(xi)的可靠性,可知它们算得的s(xi)的自由度vi如表2.6-1。
表2.6-1 彼得斯、极差、最大误差、最大残差法自由度

(3)分组极差法
对xi独立测mi组,每组ni次,得各组为
xi(1,j),xi(2,j),…xi(ni,j),(j=1,2,…,mi)
算各组最大值与最小值之差,得极差
wi(1),wi(2),…,wi(mi),
平均极差

对最佳值
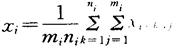
其标准不确定度

而c系数由表2.4-4取m=mi,n=ni查出。
s(xi)的自由度见表2.6-2。
表2.6-2 分组极差法自由度

2.一个量的不等精度独立测量
当对一个待求量Xi作不等精度独立测量,得
xi1(权pi1),
xi2(权pi2),
…
xini(权pini)
则最佳值

其标准不确定度

s(xi)的自由度
vi=ni-1
3.最小二乘法
Xi的最佳值xi可得自最小二乘法。
在最小二乘法中,若待求向量为 ,且xi是Z的一个分量,比如第一个分量,又测量向量为
,且xi是Z的一个分量,比如第一个分量,又测量向量为  。对误差方程
。对误差方程
AZ=L+V 权P
正规方程及解为
A′PAZ=A′PL
Z=(A′PA)-1A′PL=(qij)A′PL
由V=AZ-L,得单位权标准差

于是
xi=z1

而s(xi)的自由度vi=n-t。
【参考文献】:
[1]王立吉,计量学基础,中国计量出版社,1988。
[2]BIPM、IEC、IFCC,IUPAC,IUPAP,OIML,Guide to the Expression of Uncertainty in Measurement, ISO,1993.
[3]刘智敏,不确定度原理,中国计量出版社,1993。
[4]刘智敏,误差分布论,原子能出版社,1988。
[5]刘智敏,误差与数据处理,原子能出版社,1983。
[6]Liu Zhimin(刘智敏),Measurement Uncertainty and Its Correlation Combination,Proceeding of ISEM, 1993.
[7]国家计量总局量值传递处编,计量技术考核纲要,计量出版社,1981。
[8]国家技术监督局审定,刘智敏等编审,全国计量检定人员考核统一试题集第六分册三,误差及数据处理,陕西科学技术出版社,1990。