交直流转换技术
出处:按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第335页(7077字)
由直流量传递到交流量是通过交直流转换器件(或标准)来完成的。(6.5-4)和(6.5-5)式分别给出了交直流电流和电压的关系,这是通过作用在电阻上的电流或电压的热效应将交流量和直流量联系起来的。实现交直流转换的方法很多,下面对常用的几种方法予以简单介绍。
1.有效值的转换
有效值转换方法的基本原理是:用一种其输出正比于有效值的器件,分别通以交流和直流电进行测量。由于直流电的有效值就是其本身,所以,这种器件通以交流或直流时输出相等,这时就可认为交、直流的有效值相等,或者说,得到了以等价的直流值表示的交流有效值,即完成了有效值的交-直流转换。
(1)热电式交直流转换器件
由焦尔-楞次定律可知,电流的热效应正比于电流的有效值的平方,所以用热电效应来进行有效值的交-直流转换是一种普遍使用的方法。这种方法具有准确度高、灵敏度高、稳定性好、频率范围宽、测量范围广等优点。常用的热电变换器范围约为2~500mA,是一个小真空玻璃泡,里面密封一根加热丝,它的中点通过一个微小的绝缘珠与热偶的热端实现热的连接。当加热丝通过电流时,由于电流的热效应使加热丝温度升高,热电偶就输出一个热电势。若对加热丝分别通以交流和直流,使热电偶的输出相等,即可认为交流电流的有效值等于直流电流。
常用的交-直流热电变换器为单结结构,即用于测量加热丝热量的热偶只有一个,如图6.5-1所示。其交-直流转换的准确度为10-5~10-6量级,使用频率可到10MHz,也可以使用在更高的频率下,但误差也将与频率的平方成正比地增加。此外,加热丝中部粘接了热偶后,由于汤姆孙效应和帕尔帖效应的影响,使热偶两边加热丝的温度出现了不对称的现象,增加了交-直流转换的误差,虽然可以通过在直流电流正反向下测量取平均值的办法使这项误差减小,但单结热电变换器的准确度的进一步提高仍然受到限制。采用多结交-直流热电变换器,可克服这一缺点。它的结构基本与单结热电变换器的相同,不同的是它采用了约50个热电偶串联起来,两边各5个作为保护热偶用。这样,中间的40个热偶所对应的加热丝的温度梯度极小,大大减少了上述两个效应的影响,交-直流转换的准确度可达到10-6~10-7量级。但其频率特性较单结的差,一般只使用在100kHz以下。我国的交-直流转换基准采用的就是这种多结热电变换器,在40Hz~15kHz范围内,交-直流转换不确定度小于1×10-6。

图6.5-1 单结交-直流热电变换器
还有一种称为薄膜型的热电变换器,是利用制造集成电路的技术将加热丝和热偶都集成在一块小基片上而成,目前有的已做到200多个结。它的频率性能介于单结和多结变换器之间,可使用到1MHz以上,不确定度也可达到10-6~10-7。
从物理本质上说,用热电变换器实现的是电流的有效值的转换,若在电流回路中串联一个高质量的标准电阻,也可将电流量转换为电压量,从而实现电压的有效值的转换。
利用热电变换器也可实现交流功率的转换。为此,要用两个变换器。一个变换i+ku的有效值,其中i和u分别为交流电流和电压的瞬时值,k为转换系数;另一个则变换i-ku的有效值。求出两个变换器的输出之差,就有
△e热=k1(i+ku)2-k1(i-ku)2 (6.5-9)
其中k1为热电变换器的转换系数。将(6.5-9)式展开,得:

此式表示两个变换器的输出之差正比于瞬时功率的平均值iu,即可实现交流功率平均值的转换。
(2)热电式交直流功率比较仪
利用热电变换器进行交直流功率比较时,如果cosφ≠1,热电变换器通过交流电流和通过直流电流时加热丝温升不同,输出热电势就不相等。因此用这种方法比较交直流功率只适用于交流电路的功率因数cosφ〉0.5的情况。为了使这种方法适用于功率因数cosφ>0.1的情况,必须采取辅助措施。图6.5-2给出的即是适用于比较功率因数cosφ〉0.1的热电式交直流功率比较仪原理线路。其测量原理为:

图6.5-2 热电式交直流功率比较仪
在比较仪上加交流电压、电流,调整通过辅助加热丝rH的直流电流Ig,使检流计指零,此时辅助加热丝rH上消耗的直流功率Pg为热电变换器1及2的加热丝RH上消耗的交流功率差,即Pg=P1AC-P2AC。然后在比较仪上加直流电压、电流,并保持Pg不变,调整所通过的直流电流大小,使检流计再次指零,则:
Pg=P1DC-P2DC=RH(Ii+Iu)2-RH(Ii-Iu)2
得 KU(DC)·I(DC)=4RHIuIi
此方法的一个缺点是,交流功率和作为标准的直流功率的比较是通过一个辅助功率Pg经两次比较实现的,这样,辅助电流Ig的不稳定性直接影响比较的准确度。而且两个热电变换器一个为单加热丝,另一个为双加热丝,变换系数也不可能做得完全相同,因此其准确度不可能做得很高。图6.5-3所示线路则克服了这些缺点。这是我国独创的用于交流功率和电能基准的双桥功率比较仪,仪器中所用的两个热电变换器均为双加热丝结构,每个变换器中的一根加热丝构成类似于图6.5-2的桥式功率比较仪,则共可构成两个桥式比较仪。其测量过程为:当上桥的加热丝R1T和R2T分别通以交流电流(ii+iu)和(ii-iu)时,下桥的加热丝R3T和R4T则分别通以直流电流(II-IU)和(II+IU),调节直流电流和电压使检流计指零,则交流功率就等于直流功率。然后进行反向测量,还可上下桥交换测量,即上桥改为通直流,下桥通交流,这样,使每根加热丝都经历(ii+iu)、(ii-iu)、(II-IU)和(II+IU)四种工作状态。最终测量结果取四次比较的平均值,可消除掉大部分系统误差,获得较高的准确度。由于电能即是功率对时间的积分,该线路与时间测量相结合,即可实现交流电能与直流电能的高精度比较。以图6.5-3的线路为基础构成的国家电能基准的总不确定度为1.22×10-5。

图6.5-3 热电式双桥功率比较仪
(3)其它形式的有效值变换
除了热效应,电的力效应也可用作有效值变换。例如,两个通以相同电流的线圈之间的电动力正比于电流的有效值,两个电极之间的静电力正比于电极间电压的有效值。因此,均可用于有效值变换。利用线圈间电动力进行变换的仪器称为“电动力计”。静电力式变换器主要用于高压测量。这种利用电流力效应的有效值转换仪表,基本上都是指针式仪表,由于其结构复杂,准确度不如热电变换器高,现在已很少使用。但也有特殊的情况,如德国物理技术研究院(PTB)在电动系交直流功率转换的基础上利用光电和电子技术,使交流功率基准装置的总不确定度达到了1.2×10-5。图6.5-4为其原理线路图。

图6.5-4 PTB的电动系交直流功率转换测量系统简图
图6.5-5所示的是另一种用电流比较仪和热电式电压变换器相结合的电能标准。该方法通过电流比较仪将流过标准电度表(或瓦时计线圈)的电流缩小100倍在与次级串联的电阻上产生压降进行测量,该电阻在直流下检定并已知其交直流误差,加在标准电度表上的电压则通过热电式电压变换器与直流电压进行比较确定。这样,把电能测量直接归结为电压、电阻和时间的测量。倒相电路及电容支路是用在功率因数为0.5的情况,当把开关合上时,流过电流比较仪次级的电流Is=Ir+Ic滞后于电压π/3。美国NIST和我国的电力科学研究院均采用了这种方法,达到的不确定度分别在(3~10)×10-5左右。

图6.5-5 电流比较仪式的电能标准装置电路示意图
2.平均值的转换
一般说来,交流电量的平均值为零,不含直流分量。这里所说的平均值是指把交流电量取绝对值后的直流分量。其表达式如(6.5-6)所示。

图6.5-6 全波桥式整流器及整流元件的正向压降
为了进行平均值的转换,首先要将交流电量取绝对值,然后求出取绝对值后的直流分量,即其平均值。最常用的取交流电量绝对值的方法是全波整流法,如图6.5-6所示的用半导体二极管构成的桥式整流器。但二极管上总有一定的正向压降,影响转换准确度。所以,应尽量选取正向压降较小的器件(如常在普通万用表中用来整流的氧化亚铜整流器)。
在转换准确度要求较高时,还可采用如图6.5-7所示的用运算放大器补偿正向压降的方法。桥式整流器和整流负载电阻RL串联在放大器的反馈支路中,当放大器的开环放大倍数足够大时,O点为虚地点,电位为零。因此,流过电阻R1的电流为:

图6.5-7 用运算放大器改进平均值转换的准确度

此电流必然流过整流电路及负载电阻RL,即R1和RL实际上为串联连接,由于整流桥路的作用,RL上的电压总是同一方向的,即取了绝对值,其大小为:

整流元件上的正向压降已为放大器的输出电压所补偿,不再影响测量结果。
对整流后的电压取平均值的方法有多种,如可用滤波的方法,或者进行采样后送入计算机计算,等等。目前,用整流法进行交流电量平均值转换的准确度在音频范围(20Hz~20kHz)内约为10-4量级。
3.峰值的转换
从整流理论中可知,若在整流器输出端的负载上并联一个较大的电容(如图6.5-8所示),由于电容的储能作用,负载RL上的电压将接近交流输入电压U入的峰值。因此,这种方法可以用于进行交流电压峰值的转换。图6.5-8的电路同样存在整流元件正向压降引起的误差,此外,当整流元件不导电的时间间隔内,电容C上的电荷将通过RL泄漏一部分,使RL上的电压总比U入的峰值低一些。

图6.5-8 整流电路
解决上述困难的方法之一,也是应用运算放大器。如图6.5-9所示,在U入接近峰值期间,二极管导通,电容C充电。此时通过电阻R1和R2的反馈,构成了输入和输出成比例的反馈系统,则输出电压为
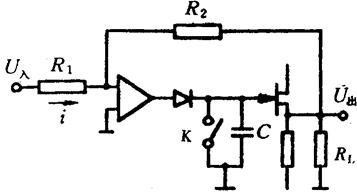
图6.5-9 用运算放大器改进峰值测量的准确度

当U入经过峰值后下降时,二极管关闭,C上保持充有的电荷。由于场效应管跟随器的输入阻抗很高,在二极管不导通的期间,基本上不会有电荷的泄漏,这样,输出电压就能以较高的准确度反映输入电压的峰值。二极管的正向压降同样已为运算放大器所补偿。图中的开关K用于在必要时释放电容C上储存的电荷。
由于微处理器、模/数和数/模(A/D及D/A)转换及计算机等技术的发展,上述交流电量的有效值、平均值和峰值的转换,均可通过对被测交流电量的波形进行采样和分析计算解决。
【参考文献】:
[1]国家技术监督局发布,GB3100~3102-93量和单位国家标准,中国标准出版社,1994年12月。
[2]王江主编,现代计量测试技术(第18章电磁计量技术),中国计量出版社,1990年12月。
[3]程守洙、江之永主编,普通物理学第二册,人民教育出版社,1979年2月。
[4]俞大光编,电工基础,人民教育出版社,1958年9月。
[5]Г.И.阿塔别柯夫,线性电路理论,人民教育出版社,1963年12月。
[6]C.A.狄苏尔、葛守仁,电路基本理论,人民教育出版社,1979年1月。
[7]乔蔚川、刘瑞珉、沈平子,The Absolute Measurement of the Ampere by Means of NMR,IEEE Trans.Instrum.Meas.,vol.IM-29,No.4,Dec.,1980.
[9]张钟华等,NIM用计算电容测定的量子化霍尔电阻的SI值(英文),计量学报,第16卷,第1期,1995年1月。
[10]刘瑞珉、刘恒基、金惕若等,NIM对γ′p及2e/h的SI值的最新测定结果(英文),计量学报,Vol.16,No.3,1995年7月。
[11]B.P.Kibble。I.A.Robinson and J.H.Belliss,A Realization of the SI Watt by the NPL MovingCoil Balance,CCE Documents 88-16,1988.
[12]P.T.Olsen。R.E.Elmquist,E.R.Williams,G.R.Jones and V.E.Bower,A Measurement of the NBS Electrical Watt in SI Units,CCE Documents 88-37,1988.
[13]Report of the 18th Meeting of CCE,1988.
[14]B.P.Kibble,I.A.Robinson and J.H.Belliss,The New NPL Moving Coil Balance-A Progress Report,CCE Documents 92-61,1992.
[15]唐统一、张钟华、张叔涵主编,近代电磁测量,中国计量出版社,1992年8月。
[16]袁楠、沈平子编,电磁量的单位制和单位的复现与传递,机械工业出版社,1986年4月。
[17]阮永顺、迈淑琴、王晓超编着,交流电桥检定与测试技术,中国计量出版社,1991年5月。
[18]唐佐梁、梁德正等,电能计量手册,河南科学技术出版社,1990年12月。
[19]K.J.Lentner.A Current Comparator System to Establish the Unite of Electrical Energy at 60 Hz,IEEE Trans.Instr.Meas.Vol.23,No.4,p.334-336,Dec.,1974.
[20]ю.B.阿法拉谢耶夫等着[苏],张伦译,磁场参数测量器具,科学出版社,1983。
[21]p.Φ.阿克纳叶夫、Л.И.留必莫夫、A.M.巴纳休克-米罗维齐着,李绍贵,王登安译,电磁量计量器具的检定,中国计量出版社,1992年5月。