信号的频谱和调制
出处:按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第365页(2961字)
1.信号的频谱
在无线电的实际应用中,许多信号都是非正弦的。对于周期性非正弦信号,我们可以用富氏级数把它们分解成许多正弦信号的叠加。在数学上,如果周期为2π的函数f(ωt)在|ωt|≤π上满足狄氏条件(工程上的函数大多满足这个条件),则可以把函数f(ωt)写成如下的富氏级数:

当k=0时,ψk=0, ,为信号的直流分量;当k=1时,A1cos(ωt+ψ1)为信号的基波(一次谐波)分量;当k=2时,A2coS(2ωt+ψ2)为信号的二次谐波分量,依次类推。k≥2的谐波称为高次谐波;k=1,3,…的谐波称为奇次谐波;k=2,4…的谐波,称为偶次谐波。
,为信号的直流分量;当k=1时,A1cos(ωt+ψ1)为信号的基波(一次谐波)分量;当k=2时,A2coS(2ωt+ψ2)为信号的二次谐波分量,依次类推。k≥2的谐波称为高次谐波;k=1,3,…的谐波称为奇次谐波;k=2,4…的谐波,称为偶次谐波。
如果把式(7.2-21)写成复数形式为:

式中 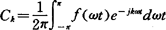 (7.2-23)
(7.2-23)
Ck与ω的关系,即信号的幅度随频率改变的关系如图7.2-7所示,这样的幅频特性图称为频谱图。

图7.2-7 信号的幅度频谱
2.信号的调制
为了用无线电信号传送声音、图像、字符等信息,必须将包含被传送信息的低频信号调制到高频电磁波上,以高频电磁波作为运载工具实现远距离传送。被运载的低频信号称为调制信号(fm),用来运载信号的等幅高频波称为载波(f0),经调制的高频波称为已调波。
对于式(7.2-1)所描述的高频波的三个参数:幅度、角频率和相位,用调制信号控制其中任一参数,分别构成幅度调制,简称调幅(AM);频率调制,简称调频(FM)和相位调制,简称调相(PM)。由于频率对时间的积分即是相位,所以调频和调相又统称为调角。
(1)调幅波的波形和频谱
调幅波的波形如图7.2-8,其中(a)为载波uc(t)=Uccosωct;(b)为调制信号um(t)=UmcosΩt;(c)为已调幅波u(t)=Uc(1+mcosΩt)cosωct,式中m=Um/Uc,称为调幅系数或调幅度。

图7.2-8 调幅波的波形
对于正弦波调制,调幅波的频谱为
u(t)=Uccosωct

由上式可见,正弦波调制的调幅波由三个频率分量组成,第一项为载波分量;第二项的频率为(ωc+Ω),称为上边频分量;第三项的频率为(ωc-Ω),称为下边频分量。上、下边频分量的幅度均为载波幅度的m/2倍。已调幅波的频带宽度为调制频率的二倍。
(2)调频波的波形和频谱
调频波的波形如图7.2-9,其中(a)为载波uc(t)=UccoSωct(b)为调制信号um(t)=UmcosΩt;(c)为已调频波u(t)==UccoS(ωct+mfcoSΩt),式中mf=Δω/Ω,称为调频指数,而Δω=KfUm,其中Kf为比例系数,Δω是调频波瞬时角频率ω与载波平均角频率ωc的最大偏移值,它仅与调制信号幅度Um有关,与角频率Ω无关。Δf=Δω/2π,称为频偏。

图7.2-9 调频波的波形
对于正弦波调制,调频波的频谱为
u(t)=Uc{J0(mf)cosωct+J1(mf)[cos(ωc+Ω)t-cos(ωc-Ω)t]
+J2(mf)[coS(ωc+2Ω)t+coS(ωc-2Ω)t]
+J3(mf)[coS(ωc+3Ω)t-cos(ωc-3Ω)t]
+… (7.2-25)
式中Jn(mf)是宗数,为mf的第n阶第一类贝塞尔函数。
式(7.2-25)表明,在单一频率调制下,调频波的频谱由载频(式中第一项)和无穷多对旁频分量组成。通常称mf≤1的情况为窄带调频,其实际带宽为2fm;称mf>1的情况为宽带调频,其实际带宽为:
2(Δf+fm)=2(mf+1)fm (7.2-26)
即忽略小于载波幅度10%的旁频分量后的频带范围。
【参考文献】:
[1]王立吉、金国钧编着,高频电压的计量测试,计量出版社,1986。
[2]李世雄、彭幼伯等编着,低频电压的计量测试,计量出版社,1988。
[3]冯新善、吴幼璋等编着,高频、微波功率的计量测试,计量出版社,1987。
[4]张关汉、李光仪等编着,高频集总参数阻抗的计量测试,计量出版社,1986。
[5]胡希平、李湘编着,微波阻抗与反射的计量测试,计量出版社,1988。
[6]蔡新泉、关志仁等编着,高频、微波噪声的计量测试,计量出版社,1988。
[7]郭允晟、苏秉炜等编着,脉冲参数与时域测量技术,计量出版社,1989。
[8]吴毅、都世民等编着,高频、微波场强和干扰的计量测试,计量出版社,1986。
[9]谢上次、徐燕清编着,高频、微波相移的计量测试,计量出版社,1992。
[10]艾明、吴达慎等编着,失真与调制参数的计量测试,计量出版社,1989。
[11]黄福芸等主编,计量知识手册,中国林业出版社,1986。
[12]陈国瑞、华荣喜等编,工程电磁场与电磁波,西北工业大学出版社,1990。
[13]Ghose,R.N.,Microwave Circuit Theory and Analysis,McGraw-Hill Book Company,Inc.,1963。