几何光学中的一些基本原理和定律

出处：按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第464页（4072字）

1．光的直线传播原理

当光波波长比所遇到的物体的线度小得多时，光在均匀介质中沿直线传播，光的行踪可以用一条直线来表示。这时可用几何作图方法来描述光的反射、折射等问题。

2．光传播中的独立性原理

几条光线在空间某一点相遇时，彼此不发生影响，相交后各按原来的方向前进。即几条光线互不相干。这在通常情况下都是正确的，但对于相干光，则相遇时发生干涉现象。

3．反射定律

光线在两种介质的分界面处将发生反射，反射光线必在法线和入射光线所成的平面内，且反射角等于入射角。

4．折射定律

在两种各向同性的均匀介质的分界面上，光线将会发生折射，光线从第一种介质进入第二种介质时，前进方向发生偏折，折射光线位于入射光线与法线所成的平面内，且入射光线和折射光线分居于法线两侧。入射角i₁的正弦与折射角i₂的正弦之比为一常量，其值与入射角的大小无关，仅决定于两种介质的性质，即

式中n₂₁称为介质2对介质1的相对折射率，n₁、n₂分别为介质1和介质2的绝对折射率。绝对折射率等于光在真空中的传播速度C与在介质中的传播速度V之比：

折射率是光波波长的函数，同一种介质对不同波长的光线，其折射率是不相等的。折射率受温度的影响，有些介质(特别是液体)，温度系数较大，另一些物质(如石英玻璃)温度系数很小。表9．2－1为几种常用介质的折射率

表9．2－1 几种常用介质的折射率

(a) 几种光学玻璃的折射率(温度为20℃，波长为587．7nm)

(b) 熔融石英在不同波长的折射率(温度为20℃)

(c) 海水在不同温度下的折射率(盐度20%，波长589．3nm)

5．全反射临界角

折射率较大的介质称为光密介质，折射率较小的介质称为光疏介质。当光线从光密介质射入光疏介质时，折射角i₂大于入射角i₁。当入射角逐渐增大，使折射角达到90°时，折射光线消失，光线被全部反射，发生全反射现象。从式(9．2－5)，可以计算出刚刚发生全反射时的入射角i_m：

i_m称为全反射临界角。以大于i_m的角度入射的光线，将被全部反射回原介质中去。光学仪器中所用的许多种棱镜及光导纤维，都是利用全反射现象而使光线改变传播方向。

以常用的K₉光学玻璃为例，全反射临界角i_m=sin^－1(1．00027／1．51637)=41°15′，如果用K₉玻璃制成一个45°的直角三棱镜，可使光线偏折90°而光能量损失很小，在光学仪器中很常用。

6．三棱镜的分光原理

透明光学材料的折射率随波长而变，定义为材料的色散率，用光学玻璃、荧石或熔融石英玻璃制成三角形的棱镜，由于棱镜材料对短波光线的折射率大，对长波的折射率小，入射光因而被分解为光谱。如图9．2－1，假定有一个顶角为a的棱镜放在空气中使用，它对某一波长的折射率为n入射光线的入射角为i₁，定义出射光线与入射光线的夹角δ为光线的偏向角，由几何关系可得：

图9．2－1 三角棱镜的色散作用

δ=(i₁－i₁′)+(i₂′－i₂)=i₁+i₂′－a

用折射定律公式可求得i₂′，于是

将上式对波长微分可得：

式中 称为棱镜的角色散率，它正比于顶角a及材料的色散率。

7．光线在球面上的折射

当光线从一种介质进入另一种介质，而两种介质的分界面是球面的一部分时，所产生的折射现象称为单球面折射。

在图9．2－2中，折射率分别为n₁和n₂的两种介质的分界面∑是球面，球心为C点，球半径为r，在光轴上有一物点O，它发出一条近轴光线OM，经界面折射后沿MI方向前进，与光轴相交于I点，若物距OP用u表示，象距PI用v表示，经过推导可得：

图9．2－2 单球面折射

若轴上某一点所发出的光经球面折射后成象于无究远，则该点称为物方焦点，该点到球面顶点P的距离称为物方焦距，用f₁表示。令式(9．2－8)中的v=∞，则此时的u值即为f₁：

同理可得象方焦距f₂

8．薄透镜公式

若折射率为n的透镜置于折射率为n₀的介质中。则可两次使用式(9．2－8)而得到薄透镜公式：

分别令u=∞或v=∞，可得前后焦距的表达式f₁=f₂=f：

要想磨制有一定焦距的单透镜，需要用这个公式，一般透镜在空气中使用，则令n₀=1；标准透镜就是这样设计的。

由上两式可得薄透镜的一般公式(即高斯公式)：

f为正值时，称为正透镜，这种透镜中间厚边缘薄，故也叫凸透镜，对光线有会聚作用。f为负值时，称为负透镜，边缘厚中间薄，也叫凹透镜，对光线有发散作用。

若两个(或多个)薄透镜很靠近地放在一起组成一个共轴复合透镜，则组合后的透镜组的焦距f与原来两个透镜焦距f₁、f₂的关系如下：

焦距的倒数表征透镜屈折光线的能力，当f用米为单位时，1／f之值称为透镜的屈光度。正透镜的屈光度为正值，负透镜的屈光度为负值，两个薄透镜叠在一起，总屈光度等于每个透镜屈光度的代数和。

9．球面反射镜的成象

一束平行光射到凹球面反射镜上可以会聚，射到凸球面反射镜上，光束会发散。用反射定律就可以推导出球面反射镜的成象公式，公式与高斯公式的形式是一样的，只是正负号的规定有所不同。

若有一近轴的平行于光轴的光束射到曲率半径为r的凹球面反射镜上，它将会聚于光轴上的一点，焦距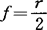。用凹球面反射镜成象时，由于物与象会互相遮挡，故在实用中往往让物稍稍偏离光轴，象成在光轴的另一侧。只要物距大于f，均可得到一个倒立的实象，情况与正透镜相似。

凸球面镜的成象情况与负透镜相似，汽车的后视镜就是一个应用例子。

球面反射镜成象系统的第一个优点是与光波的波长无关。不管什么波长的光，反射角总等于入射角，组成一个系统后，对什么波长的光都适用。故宽波段的仪器，必须采用反射式成象系统。因为任何透镜材料的折射率都是波长的函数，不同波长的光线的成象位置一定会有些差别(即透镜的色象差)。反射系统的第二个优点是较易制造大通光口径的反射镜，以增大接收光能量的本领。而在制造大口径的透镜时因受材料的限制而变得十分困难。

【参考文献】：

［1］现代计量学概论，鲁绍曾主编，中国计量出版社，1987。

［2］现代计量测试技术，王江主编，中国计量出版社，1990。

［3］光度学，郝允祥等编着，北京师范大学出版社，1988。

［4］色度学，荆其诚等编着，科学出版社1979，。

［5］Principles Governing Photometry，Metrologia，19，97－101，1983．

［6］Accurate Measurement and Correction for Nonlinearities in Radiometers，J．Res．NBS，67A，1972．