农作物有害生物统计种类和方法
出处:按学科分类—农业科学 中国农业出版社《植物保护统计手册》第220页(5459字)
一、统计种类
农作物有害生物种类繁多,为便于工作,将有害生物分为农作物病虫、杂草、害鼠三大类进行统计。
(一)农作物病虫害 各种农作物上有多种病虫发生,如全国水稻害虫300种,棉花害虫超过300种,仅据山东调查小麦病虫148种(害虫117种,病害31种)。但这些病虫并非都造成明显的经济损失,甚至有些害虫不但为害轻,还是繁殖自然天敌的食物,造成经济损失的只是少数主要病虫。有些次要病虫通过防治主要病虫而得到兼治。因此,统计的对象应当是农作物上分布范围广、发生面积大、危害损失重的主要病虫。目前全国范围统一统计的病虫(除检疫对象)共67种,其中水稻病虫7种,麦类病虫9种,其他粮食作物(玉米、高粱、谷子、大豆等)病虫7种,棉花病虫7种,油料作物(油菜、花生等)病虫6种,果树病虫7种,蔬菜病虫12种,其他经济作物(甜菜、烟草、甘蔗、茶等)7种,杂食性害虫5种。
由于各地的地理位置、气候环境、作物种类不同,病虫种类、种群数量和危害程度各异,所以除上述病虫必须进行统计外,各省(自治区、直辖市)的主要病虫也应作为各自的统计对象加以统计。
(二)农田草害 由于一种作物田内多种杂草混生共同影响作物的生长发育,因此,不分草种而按作物种类分别统计。
(三)农田鼠害 害鼠在它的孳生地活动范围大,并且可能同时为害多种作物,所以对农田害鼠的统计,不分鼠种,不分作物,而按行政区进行统计。
二、统计方法
(一)抽样 对有害生物统计原始资料(数量特征信息)的取得,过去常用经验估测的办法,由于误差大不宜再用。但又不可能对所有作物田块进行全面调查,而只能根据有害生物的分布特点,采用适宜的取样方法,从研究的总体中抽取一定数量的个体(样本量)所得的结果来估计总体的结果。合理的提取样本,是有害生物统计的基础,正确的取样方法应该使总体内每一个体被抽取为样本的机会相等。为了使抽取的样本能更好地代表总体,根据有害生物统计任务及其特殊性,在抽样方法上可采用分段抽样与随机取样相结合的方法,即:以县作为研究的总体,根据影响有害生物发生的生态因素划分不同类型的抽样调查区,每个调查区再选定20%有代表性的乡作为样点乡,每个样点乡再选定若干片,每片随机抽样调查不同类型田(如早、中、晚播田,或长势1、2、3类田),在每一田块中根据有害生物分布型采用棋盘式、对角线5点式或平行线式,或“Z”字形随机取样调查。
在取样调查中确定取样方法后,还需进一步确定样本调查量,才能保证所获得平均数(或百分率)符合预定的允许误差范围。可从置信范围统计中得到比较准确的估计。抽取的样本量和允许的准确度之间的关系可用以下公式表达:
如用平均数表示则:

如果以百分率表示则:

式中:t值以“t”值表中查得:自由度=∞,P=0.05时,t=1.96;P=0.01时,t=2.58;标准差“S”或“Sp”为正式调查前在预备调查中实际查得的;μ为总体平均数(期望值),“π”为总体百分率;( )或(P-π)是允许误差(即
)或(P-π)是允许误差(即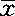 或P偏离μ或π的差数)是调查前根据需要预先定的。
或P偏离μ或π的差数)是调查前根据需要预先定的。
例题1 调查小地老虎幼虫的虫口密度,预先调查336平方米,平均每平方米幼虫4.77头,S=2.54头,要求允许误差不超过1头/平方米,并以95%的可靠度保证其误差范围,需取多少点为宜?
查t表:t=1.96,代入公式(1)
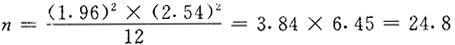
即取25平方米所得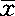 与实际总体μ之间相差有95%的把握,每平方米不超过1头。
与实际总体μ之间相差有95%的把握,每平方米不超过1头。
例2 预先调查三化螟白穗率,用双直线平行跳跃取样,全田抽查200穴,共查1350株,平均白穗率1.2%,允许误差不超过0.5%,并有99%可靠度,需取多少株水稻?
查t表,P=0.01时,t=2.58,代入公式(2)得:

即需要取样3156株才能达到预定的要求。
(二)调查资料的统计分析 田间抽样调查在于获得信息(样本数据资料),而数据的统计分析则在于辩识信息。因此,研究由样本观察值经过计算分析得到的样本特征数(统计量)与总体参数的关系,进而由样本对总体的推断,就成为统计分析的中心任务。样本特征数可分为反应数据集中程度的特征数——平均数和反应数据变异程度的特征数——变异数两大类。
1.平均数 是一个重要的数量指标,是数据资料的集中性代表值,可以表示资料中各变量的中心位置,并可作为一组资料与另一组资料相差比较的代表值。常用的平均数有算术平均数、中位数、众数、几何平均数、调和平均数(倒数平均数)、平均拥挤度等,但最常用的是算术平均数(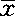 ),它服从于正态分布。直接算法的公式为:
),它服从于正态分布。直接算法的公式为:

如果所调查的几个数值都代表有不同程度的比重时,统计学上称这个比重为权,在计算平均数时应采用加权法。其计算公式为:

式中:fi代表权数,在频数分布表中为各组的频数(观察值出现次数);xi为观察值,在频数分布表中表示各组的组中值;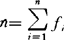 为权数总和,在频数分布表中表示总频数(总次数)。
为权数总和,在频数分布表中表示总频数(总次数)。
2.变异数 是表示样本平均数( )变异程度的特征数,常用的有方差、标准差、变异系数。
)变异程度的特征数,常用的有方差、标准差、变异系数。
(1)方差 是表示样本平均数( )变异量大小的特征数。(
)变异量大小的特征数。( )为离均差,将各离均差平方即消除了负号又加重较大离均差的分量,借以增加度量变异度的灵敏性,各离均差平方值之和叫平方和即
)为离均差,将各离均差平方即消除了负号又加重较大离均差的分量,借以增加度量变异度的灵敏性,各离均差平方值之和叫平方和即 ,用样本数除平方和得到平均平方和,简称均方或方差。其公式为:
,用样本数除平方和得到平均平方和,简称均方或方差。其公式为:

在大样本(n>30)的情况下,可以说S2是相应总体方差σ2的无偏估计值。 ,即S2=σ2;但当所抽取样本为小样本(n≤30)时,样本方差与总体方差有较大的编离,即S2<σ2但这种差异随着n增大而减少,其关系为
,即S2=σ2;但当所抽取样本为小样本(n≤30)时,样本方差与总体方差有较大的编离,即S2<σ2但这种差异随着n增大而减少,其关系为 ,则
,则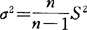 ,把“
,把“ ”称修正样本方差,以S2*表示,其公式为S2*:
”称修正样本方差,以S2*表示,其公式为S2*:
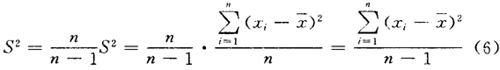
所以S2*才是总体方差σ2的无偏估计值。上述公式计算麻烦,可简化为:

(2)标准差 就是方差的平方根,用以表示资料的变异程度,其单位与观察值的度量单位相同,定义公式为:

上式计算较麻烦,其计算公式为

如果样本平均数是用加权法计算,标准差也应用加权法计算。即

(3)变异系数 是一个无量纲的比率,便于样本间的相互比较,它是样本标准差(S)和平均数( )的百分数,以CV表示,即:
)的百分数,以CV表示,即:

3.参数估计 是研究如何根据样本统计量估计总体参数的问题。
(1)点估计。是以样本统计量作为相应总体参数的估计值的问题。已经证明,样本平均数(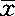 )是总体期望值μ(总体平均数)的无偏估计量,前面已证明大样本方差S2和小样本修正方差52*是总体方差σ2的无偏估计量。
)是总体期望值μ(总体平均数)的无偏估计量,前面已证明大样本方差S2和小样本修正方差52*是总体方差σ2的无偏估计量。
(2)参数的区间估计(平均数的置信限)。样本平均数( )是一个随机变量,往往受抽样误差的影响其取值总是围绕着总体待估参数值(μ)摆动,因此点估计不免有偏差,所以总体待估参数的取值应是一个可以变化的区间,并给一定概率(95%-99%)以保证其可靠程度。就是说,区间估计就是在一定概率保证下由样本统计量估计总体参数可能存在的范围。这个范围叫“置信区”;给出的概率P=1-α叫置信水平,置信区间以外的概率(α)谓显着水平。当α取5%,置信概率为95%,以μ=0.95表示;a取1%,置信概率为99%,以μ=0.99表示。平均数标准差
)是一个随机变量,往往受抽样误差的影响其取值总是围绕着总体待估参数值(μ)摆动,因此点估计不免有偏差,所以总体待估参数的取值应是一个可以变化的区间,并给一定概率(95%-99%)以保证其可靠程度。就是说,区间估计就是在一定概率保证下由样本统计量估计总体参数可能存在的范围。这个范围叫“置信区”;给出的概率P=1-α叫置信水平,置信区间以外的概率(α)谓显着水平。当α取5%,置信概率为95%,以μ=0.95表示;a取1%,置信概率为99%,以μ=0.99表示。平均数标准差 ,S
,S 和S的关系为
和S的关系为 当自由度=∞,P=0.05时,t=1.96,P=0.01时,t=2.58。
当自由度=∞,P=0.05时,t=1.96,P=0.01时,t=2.58。

当α取5%,μ=0.95;α取1%,μ=0.99时,μ的置信区间可表示为:
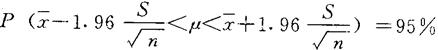
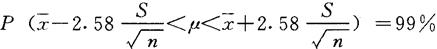
例:在麦田对角线五点随机抽取小麦100株,调查麦蚜虫口密度,平均每株有虫20头,S=5,求μ=0.95时,该麦田麦蚜总体(μ)虫口密度的置信区间。
解:为大样本n=100, ,S=5,α=0.05,代入公式:
,S=5,α=0.05,代入公式:

答:麦蚜的总体平均虫口密度(μ)在19.02-20.98之间,其可靠程度为95%。

即麦蚜的总体平均虫口密度(μ)在18.01-21.29之间,其可靠程度为99%。
4.可靠性分析(t测验) t检验是经运算求得t值来判断样本平均数代表总体参数(μ)的可靠程度的一种方法。计算t值公式为
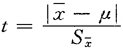
式中:| |:样本平均数与总体参数的绝对差值,|
|:样本平均数与总体参数的绝对差值,|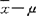 |除以(
|除以( (平均数标准差)就转换为差值与样本平均数本身误差的相对比值—-t值。当差值大误差小时,则t值大,表示
(平均数标准差)就转换为差值与样本平均数本身误差的相对比值—-t值。当差值大误差小时,则t值大,表示 与μ之间差异大,
与μ之间差异大, 值可靠性小。经过t值与其相应的概率P(在这里P指
值可靠性小。经过t值与其相应的概率P(在这里P指 与μ之间相等的可能性)之间关系的研究认为:当样本容量n>120,实际算得的t≥1.96,则P≤0.05时,可解释为
与μ之间相等的可能性)之间关系的研究认为:当样本容量n>120,实际算得的t≥1.96,则P≤0.05时,可解释为 与μ之间相同的可能性在5%以下,认为
与μ之间相同的可能性在5%以下,认为 与μ之间差异显着,
与μ之间差异显着, 不可靠,不能代表μ;当t≥2.58,P≤0.01时,则两者差异极显着,
不可靠,不能代表μ;当t≥2.58,P≤0.01时,则两者差异极显着,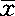 极不可靠。根据在不同自由度(n-1)下与t和P的关系,制成了t值表,在实际应用时,计算实际所得t值再按自由度查出相对应概率(P)值,按可靠性(差异显着性)标准进行比较判断即可。即:
极不可靠。根据在不同自由度(n-1)下与t和P的关系,制成了t值表,在实际应用时,计算实际所得t值再按自由度查出相对应概率(P)值,按可靠性(差异显着性)标准进行比较判断即可。即:
P≤0.05(5%)差异显着,记*(或不可靠)
P≤0.01(1%)差异极显着,记* *(极不可靠)
P>0.05(5%)差异不显着(或可靠)
例题:在棉田内调查一代棉铃虫卵量,全田平均百株卵量(μ)为16.2粒,为嵌纹分布型,试比较下列两调查方法的可靠性。①先用分行抽条取样100株,得百株平均( )卵量21粒,
)卵量21粒, 为6.3;②用双行直线跳跃取样法取样100株,百株
为6.3;②用双行直线跳跃取样法取样100株,百株 为6粒,
为6粒,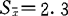 。
。

查t值表:df=n-1=100-1=99(表中无99,用100代替),t0.05=1.982,t0.01=2.575,因t0.76<t1.982;P(0.05以上)>P0.05>P0.01,不显着,可靠。

查t值表:t=4.4,其概率P<0.001,差异极显着,此法极不可靠不能采用。
5.线性回归及其方差分析(从略)