成本及其按成本习性的分类
出处:按学科分类—经济 企业管理出版社《现代企业内部会计实用手册》第912页(8194字)
一、成本习性
成本习性,亦称“成本性态”,是指成本总额与业务量(产销量)总数之间的依存关系。这种依存关系是客观存在的,表现在成本是否随着业务量的变化而变化。研究成本与业务量的依存关系,掌握其变化规律,有助于企业进行预测、决策分析,编制预算,对企业成本进行事前控制和日常控制,以及对各个责任层次的业绩进行评价与考核等。成本按其与业务量的关系进行分配是规划和控制企业经济活动的前提条件,它有利于充分挖掘企业的内部潜力,实行最优化管理,实现最佳经济效益。
按照成本习性理论,可以将企业成本分为随业务量变化而发生变化的变动成本和不随业务量变化而变化的固定成本两大类。
二、变动成本与固定成本
(一)变动成本变动成本是指成本总额与业务量总数成正比例增减变化的成本,即产量越高,变动成本总额越大;反之,则变动成本总额越小。这类成本主要是指企业生产产品所消耗的直接材料成本,直接人工成本,外购零部件支出总额。
变动成本的习性模型,通常如图表1-1和图表1-2所示。变动成本总额表现为一条从坐标圆点开始,在第一象限的直线。其坐标系中横轴代表业务量,纵轴代表在该业务量水平下所耗费的变动成本总额,两者的比率反映着变动成本与生产规模的变化关系。
图表1-1

变动成本习性模型
图表1-2

单位变动成本习性模型
从上面图示中变动成本线的列示可见,变动成本具有两个特征:(1)变动成本总额的大小是随业务量的变动成正比例增减变动的;(2)单位变动成本是不随业务量变动而变动,即不变的。
(二)固定成本
固定成本是指凡是成本总额在一定时期一定范围内不受业务量增减变化影响而固定不变的成本。如折旧费、房屋租赁费、管理人员年薪等。单位产品中的固定成本是随产品产量变化而成反比例变化。固定成本的习性模型如图表1-3和图表1-4所示。
图表1-3

固定成本总额习性模型
图表1-4
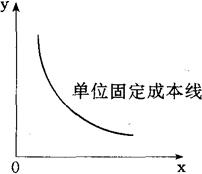
单位固定成本习性模型
图表1-3中纵轴表示成本总额,横轴表示业务量。固定成本总额的大小决定着固定成本线在Y轴上的高度,这个高度与业务量的增减变动无关,因此,固定成本是一条平行于横轴的直线。由此可见,成本总额不随业务量变化而变化是固定成本的主要特征。图表1-4中的曲线表示的是固定成本的另一个主要特征,即单位固定成本随业务量的变化而成反比例变化。
固定成本按其是否受约束分为约束性固定成本和酌量性固定成本。
约束性固定成本是指企业为了维持正常的生产活动而必须开支的固定成本。如房屋租金;保险费等。该成本的特点是:随着企业的生产能力的形成,一般在短时期内不能做大的削减,这是企业维护正常生产经营活动的必要开支,在一定的产量范围内与企业生产能力的发挥状况(即产量高低)无直接关系,一旦发生就是固定不变的。只有当企业增加或减少资产时,即改变了生产经营能力后,约束性固定成本才可能发生变化,以适应新形势的需要。对约束性固定成本的控制,一般都是通过挖掘内部生产潜力,提高生产效率,以期降低单位产品中约束性固定成本含量的办法来相对降低成本。
酌量性固定成本是指通过企业高级管理阶层的决策活动,能够决定其支出量的固定成本。如职工培训费、宣传广告费等。酌量性固定成本的特点是其成本数额可以通过管理阶层的决策活动决定其发生数额的固定成本。对于酌量性固定成本的控制,主要从其总额上加以控制,不断降低其绝对额支出。
(三)成本总额
管理会计按成本习性将成本总额分为变动成本和固定成本。其成本总额可用以下公式表示:
成本总额=变动成本+固定成本
设成本总额为y,变动成本总额为bx,固定成本总额为a,则上式可用下列方程式表示:
y=bx+a
成本总额的习性模型可用图表1-5所示。
图表1-5

成本总额习性模型
三、混合成本
混合成本是指既具有变动成本特性,又具有固定成本性质的成本。其主要特点是:成本总额随业务量的增减而发生增减变动,但其变动幅度并不与业务量成正比例增减变动;其单位成本既随业务量增加而下降但又不成反比例下降。由此可见,混合成本是兼有变动成本和固定成本两种成本特性的成本。因此,不能用单一的习性模型来表示。
(一)混合成本的分类
由于混合成本中的变动成本和固定成本的发生和变化的不同特点,形成了混合成本的不同类型。
1、半变动成本
半变动成本是指成本总额随着业务量的变动而变动,但变动的幅度不是成正比例增减,这种成本通常有一个基数,一般不变,相当于固定成本,但在这个基数上面,随着业务量的增加成本成正比例增加,这部分相当于变动成本。其成本习性模型如图表1-6所示。
图表1-6

半变动成本习性模型
2、半固定成本
半固定成本是指在一定的业务量范围内,成本不随业务量的变化而变化,只有超过这个业务量的范围,成本就会突然跌到一个新的水平,其变动幅度很大;在另一层次的业务量范围内又固定不变,直至超过这个范围进行另一次新的跳跃,如此反复变动。其特点是:成本发生的多少受到分段的业务量限制,在每段业务量范围内是固定数,但从其成本总额发生趋势来看,又具有变动成本的某些特性。例如,企业检验人员的工资,当产量在一定限量内,其工资支出是固定不变的,如果超过正常产量范围,则需新增加检验人员,这样检验人员工资支出,就会大幅度地提高。半固定成本习性模型如图表1-7所示。
图表1-7
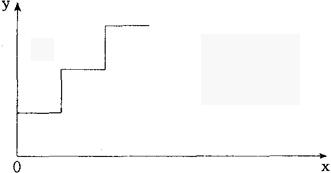
半固定成本习性模型
3、不规则成本
不规则成本是指成本总额的多少与业务量的大小之间没有一定的规律可循,但总额仍随业务量的变化而变化的成本。其成本模型如图表1-8所示。
图表1-8

不规则成本习性模型
(二)混合成本的分解方法
由于按成本习性原理将成本分为变动成本和固定成本,目的是为了更好地进行成本的规划和控制。因此,需要采用适当的方法将混合成本分解为变动成本和固定成本。其具体分解方法主要有以下几种:
1、高低点法
高低点法是指根据历史资料进行分析,从中找出其发生额最高的混合成本和最低的混合成本,以此作依据,运用数学方法,建立的代表历史资料的混合成本趋势方程式,来分解混合成本的方法。其原理是:在过去发生的产量资料和其所对应的混合成本资料中,找出这一时期的最高产量和最低产量,以及它们所对应的混合成本,然后用高低点混合成本之间的差额除以高低点业务量的差异数,求出变动率,借以将混合成本分解为变动成本和固定成本。
根据高低点法原理,其计算步骤如下:
(1)设混合成本方程式为:Y混=a+bx。
其中:Y混为混合成本总额;
a为固定成本总额;
b为单位变动成本;
c为业务量。
(2)根据历史资料找出高点(X高、Y高)、低点(X低、Y低)的坐标,并求解出业务量之差(△x)和高低点混合成本之差(△y)。
(3)求其变动率(b),即直接方程式的斜率

(4)求固定成本(a)
a=高点混合成本总额-高点变动成本总额=y高-bx高
或 =低点混合成本总额-低点变动成本总额=y低-bx低
(5)列出混合成本趋势直线方程式:
y混=a+bx
〔例〕某公司1992年1-9个月的修理费资料如图表1-9所示。
图表1-9

解:(1)根据图表1-9可求得:

(2)根据上步计算,可确定b:

(3)根据成本方程式y混=a+bx,确定a
∵y混=a+bx
∴a=y混-bx
=150000-60×20000=30000(元)
或 =90000-6×10000=30000(元)
(4)根据上述计算结果,可以得出修理费和业务量关系的趋势直线方程(即修理费混合成本)为:
y=30000+bx
高低点法的特点是:计算简单,便于应用,但是由于实际发生的数据不一定是严格按线性条件发生的,因此,在选择高低两点的数据作为列示混合成本趋势直线方程式不准确,与实际结果相比误差较大。
2、布点图法
布点图法,也称“散布图法”,是指根据若干期产量与其相对应成本的过去资料绘制出的散布图,然后用直观分析的方法划出一条穿过所有点,与所有点距离相等的一条直线的方法。其特点是直观、易行,但由于绘图的精确较差,容易引起人为的误差,故这种方法是分解混合成本的一种辅助方法。
布点图法分解混合成本的基本程序如下:
(1)将过去资料中的所有点都描到直角坐标系第一象限中。
(2)根据第一步骤,再用目测绘制出一条距所有点等距离的直线。
(3)将上述直线与纵轴的交点标出,坐标圆点到交点的距离即为该成本直线方程式中的固定成本。
(4)根据成本直线方程式y混=a+bx求解出直线的斜率(即单位变动成本b)
(5)根据求解出来的a、b列出混合成本趋势直线方程式:y混=a+bx
〔例〕根据图表1-9,用布点图法分解混合成本。
解:(1)根据资料,将某公司1-9月份所有点都描到直解坐标系中,并绘出直线如图表1-10所示:
图表1-10

(2)从上图可见固定成本约为29,000元。
(3)根据y混=a+bx
则b= 将高点值(20000和150000)代入
将高点值(20000和150000)代入

(4)混合成本趋势直线方程式
y=29000+bx
3、回归直线法
回归直线法是指数学中的“最小平方法”原理,分解混合成本的一种方法。由于布点图法是通过直线分析目测出成本点的变化趋势而划出的一条趋势直线,受人为的因素影响较大,其精确度较难控制。因此,在管理会计中,将数学中最小平方法理论引入,求出一条距所有点误差平方和最小的直线,这条直线可以精确地反映出成本的变化趋势,且是一条回归直线。
回归直线法求出的这条直线,以业务量为自变量x,混合成本为因变量y混,所成的线性关系为:
y混=a+bx
其中:a为固定成本总额;
b为单位变动成本;
bx为变动成本总额;
x为业务量;
y混为混合成本总额。
在列出混合成本与业务量的上述方程式后,就可以根据两者之间的内在联系,分解出固定成本总额(a)和单位变动成本(b),其具体方法为:
设 y=a+bx
各期混合成本与业务量的关系公式为:

把前述方程式作几个观测值的形式来表式,即得:
∑y=na+b∑x (1)
将n个观测值表示的成本与业务量关系的方程式各项分别乘以x,即得:

将上述n个乘以x的方程式加和,即得:
∑sy=a∑x+b∑x2 (2)
把(1)移项化简,即得:

把(3)代入(2),并化简,即得:

或将(1)、(2)两方程式联系,并简化,即得:

〔例〕某公司199×年1-12月份动力费资料如图表1-11所示,要求:采用回归直线法分解动力费混合成本。
图表1-11
某企业动力费及业务量

解:(1)根据图表1-11所列数据,进行加工,求出xy、x2、y2,并编制图表1-12。
图表1-12

(2)根据前列公式,将上表计算结果代入


将求解出的a和b代入直线万程式,即可建立混合成本动力费的方程式如下:
y=a+bx=210.12+19.57x
值得注意的是,采用回归直线法,业务量(x)与混合成本(y)之间必须保持良好的线性关系,在此基础上求解出来的回归直线方程式才能较准确反映成本变动趋势。因此,在采用此法时,需要先计算混合成本(y)和业务量(x)之间的相关程度。检验相关程度的方法是求解相关系数。
相关系数一般用“r”来表示,其取值范围一般在0~1和-1~0之间。
当r=0时,说明x与y两者之间不相关
当x=1时,说明x与y两者之关完全正相关
当x=-1时,说明x与y两者之间完全负相关。
r的值介乎于0~1或-1~0之间时,其数值的大小,表示其相关程度。
一般讲采用回归直线法分解混合成本,应先计算其x与y之间的相关系数,只有相关系数(即r)接近于1时,才说明x与y基本存在着线性关系,可以用直线y=a+bx来描述其成本变动趋势。
相关系数(r)的计算公式如下:

从计算结果可见,相关系数接近1,说明本题x与y是相关的,呈线性关系。