总体、样本、统计量与统计分析
出处：按学科分类—农业科学 农业出版社《水产养殖手册》第872页（2454字）
以生物数量为研究对象的生物水产科学调查和实验需要首先根据研究目的和实际情况明确规定“观测单元”，并合理规定观测单元之间的“同质”或者“随机差异”。人们以观测单元的某一种或者某几种生物数量作为研究对象，就把所研究的同质生物数量定义为总体，记号是X，Y，……，总体的观测值用相应的小写字母x’y，……表示。需要研究m种生物数量，就定义m个总体，并以它们为分量构成m元总体；如果所研究的同种生物数量随着在某一范围T内变化的数量因子x(记为x∈T，读作“x属于T”)改变，则形成总体族{Yx，x∈T}。总体族也有依赖于m(m≥2)个数量因子x1，x2，……，xm的情形，
表这m个数量因子。
总体X的取值随观测单元改变，它在所有的同质观测单元上取值的算术平均称为总体平均数，记为EX(1)，这是一个客观存在的未知常数。总体在每一个观测单元上的取值与常数EX都有差异，差异的平方(X—EX)2在所有的同质观测单元上取值的算术平均称为总体方差，记为DX
E(X—EX)2(2)，方差的算术平方根
称为总体标准差。对于二元总体(X，Y)T(3)的两个分量，σyx
E(X—EX)(Y—EY)称为总体协方差，
称为总体(线性)相关系数。
总体族{Yx，x∈T}的平均数EYx随x∈T变化形成x的某一函数，其图形称为总体族Yx关于数量因子x的回归线。只有一个数量因子x的情形称为一元回归，依赖于m(m≥2)个数量因子x1，x：，……xm的情形称为多元回归或者多重回归。对于一元与多元回归，如果采用线性模式
x=β0+βx，x=β0+
则称为线性回归，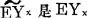
的线性模拟。某些曲线(或者曲面)回归可以通过数据变换化为线性回归，称为线性化。例如，y=dxb—→lny=lnd+blnx。
与一元线性回归不同，对于二元总体(X，Y)T的研究一般使用线性相关分析。这两种统计分析在计算方面有许多共同步骤，但概念不同，分析方法也不同。然而在实际工作中，二者常常被混用。对于某些复杂的实际问题，有时仅能借用以上两种分析的概念和一部分计算方法，一般难以进行有关的分析工作。
对于在一组r(r≥3)种生态条件，或者r种生物特性下分别产生的r个同种生物数量总体Xj，j=1—r，检验它们的平均数是否全相等并在不全相等的情形比较其大小，称为方差分析与多重比较。r=2的情形属于参数的显着性检验和区间估计的内容，EX和DX都是总体的参数。
在同质的生态条件和生物特性下相互独立地随机抽取n个同质的观测单元，总体就相互独立地n次随机取值，每一次的取值规律(概率分布)都相同。以上所述的总体X的n次独立重复X1，X2，……，Xn称为样本，n称为样本容量。样本观测值x1，x2，……，xn是n个同质数据，简记为1
n。统计量是样本的函数(以样本的n个分量为自变量)，例如：样本平均数
X1，样本差异平方和
，样本方差
，样本标准差
等。它们的观测值是样本观测
x2，……，xn)的同一个函数：
，
)2，
，
等，分别称为样本观测值的平均数，差异平方和，方差，标准差等。二元总体(X，Y)T的样本观测值
简记为
，其中的每一个数偶
，i=1-n分别是二元总体在第i个随机抽取到的观测单元上的取值(如第i尾鱼的体长和体重)。与一元总体类似，需要定义样本观测值的平均数
，
；差异平方和lxx，lyy(4)；方差
，
；标准差Sx，Sy。除此而外，还需要定义样本观测值的相关矩
(
)(
)，协方差
以及(线性)相关系数
=
。上述的各统计量的观测值把样本观测值，即总体的n次取值—n个同质数据
或者n个同质数偶(
)—所包含的关于总体的信息分别“浓缩”到一个数里面。
统计量X，S2以及二元总体的样本协方差Syx，样本(线性)相关系数r特别地称为总体参数的估计量，它们分别给出了估计总体参数EX，DX以及σyx，ρ的一种方法：用它们的观测值X，S
以及Syx，r作为相应的总体参数的估计值，称为点估计(例如，用一个世代同龄群体被采集到的n尾鱼的平均体长X作为这个世代所有尾鱼的平均体长EX的估计值)，主要用于样本容量n较大的情形。以点估计为基础，配合有关的统计量的概率分布(取值规律)，可以构造出总体的平均数与标准差的置信区间以及两个(相互独立)总体的标准差之比与平均数之差的置信区间，称为区间估计。参数的区间估计把参数的显着性检验的结论包括在内。上述的各估计量是最基本的统计量，对(正态)总体进行各种统计分析最经常使用的统计量的观测值X2，t，F，等，分别以X，SSx，S
，Sx为基本要素“组装”而成。
样本是联系总体与统计量的桥梁：一方面，样本的每一个分量都与总体的概率分布(取值规律)相同，并且相互独立，从而样本的概率分布被总体决定；另一方面，统计量是样本的函数，从而样本又决定了统计量的概率分布。这样，总体的概率分布与统计量的概率分布以样本为桥梁建立起来的必然联系使人们能够以统计量的概率分布为基础，根据统计量的观测值对总体进行统计分析。
“数理统计表”是人们根据统计分析的需要把各种统计量的概率分布数值化，其中最经常使用的是显着性检验的临界值，例如：X2分布与F分布的上侧分位数X2。(f)，Fα(f1，f2)；标准正态分布与t分布的双侧分位数uα，tα(f)，等。这些分位数与总体参数估计量的观测值是构成“置信区间”的两类基本要素。不同的统计分析问题分别需要特定的统计量。统计分析的实际工作由以下两部分组成：计算统计量的观测值；查相应的数理统计表。
(编者：刘长安 审者：孙尽善)