单因子方差分析
出处:按学科分类—农业科学 农业出版社《水产养殖手册》第896页(3249字)
对于分别在因子A的r(r≥3)个水平下产生的r个相互独立的正态总体Xk,k=1—r,方差分析要解决的问题是:以总体方差 ≡σ2,k=1—r为前提,推断总体的平均数μk,k=1—r是否全相等;如果不全相等(至少有2个μk不相等。如果是2个,是哪2个?如果有3个μk彼此不相等,是哪3个?等),则需要对它们之间相等与不相等的具体情况进行多重比较。
≡σ2,k=1—r为前提,推断总体的平均数μk,k=1—r是否全相等;如果不全相等(至少有2个μk不相等。如果是2个,是哪2个?如果有3个μk彼此不相等,是哪3个?等),则需要对它们之间相等与不相等的具体情况进行多重比较。
这里需要继续使用(48.5.7)式,它在后面写为(48.6.3)1式和(48.6.5)1第一式;并定义 nk个数据总的平均数
nk个数据总的平均数 与差异平方和SST:
与差异平方和SST:

上式定义的 是r个
是r个 k以nk
k以nk nk为权的加权算术平均数。X与SST跟§48.2定义的样本观测值的
nk为权的加权算术平均数。X与SST跟§48.2定义的样本观测值的 与sSx不同,后者跟这里的Xk与Ssk,k=1—r相同。下面,研究(48.6.1)1式定义的SST的分解:
与sSx不同,后者跟这里的Xk与Ssk,k=1—r相同。下面,研究(48.6.1)1式定义的SST的分解:

上式可以写为

需要定义下列方差和F:


在nk≡n,k=1—r情形,(48。6.1)1式和(48.6.3—5)1式转化为:

以Bartlett统计量的观测值X2< (r-1)为前提,如果F>Fa(r-1,fe),这里
(r-1)为前提,如果F>Fa(r-1,fe),这里 或者r(n-1),则r个
或者r(n-1),则r个 ,k=1—r之间的差异显着(系统差异,存在于哪些
,k=1—r之间的差异显着(系统差异,存在于哪些 k之间?),r个μk不全相等;如果F
k之间?),r个μk不全相等;如果F k,k=1—r差异不显着(随机差异),r个μk全相等,因子A的r个水平Ak,k=1—r对于人们研究的生物数量所造成的差异相当于随机因素的影响。
k,k=1—r差异不显着(随机差异),r个μk全相等,因子A的r个水平Ak,k=1—r对于人们研究的生物数量所造成的差异相当于随机因素的影响。
 式与
式与 式的计算步骤分别如表48—4(1)
式的计算步骤分别如表48—4(1)
表48—4(1)


(二)与表48—4(2)(二)所示。
表48—4(2)


下面介绍单因子方差分析的SHARP—5002计算器程序表内计算部分。下列nk≡n,k=1—r情形的(1)2与(2)也适用于本章第七节双因子方差分析表48—6的一部分表内计算。
(1)1表48—4(1),nk不全相等:



(2){ 对k=3,4,……,r依次进行。
对k=3,4,……,r依次进行。
下面介绍多重比较。这一统计分析步骤只在F>Fα(r-1,fe)情形才有必要。它分为三种类型:
(1)Dunnett法,简称D法,用于r-1个Xk分别与“对照”比较,对照记为X0:如果| k-
k- 0|>Dα(r-1,r(n-1))
0|>Dα(r-1,r(n-1)) 则
则 k与
k与 0差异显着,μk
0差异显着,μk μ0,并根据
μ0,并根据 k-
k- 0乏0推断为μk
0乏0推断为μk μ0,Dα(f1,f2)可以查“多重比较中的Dunnettt表”得到。这种方法在理论上只适用nk≡n,k=1—r;如果nk不全相等,对于|
μ0,Dα(f1,f2)可以查“多重比较中的Dunnettt表”得到。这种方法在理论上只适用nk≡n,k=1—r;如果nk不全相等,对于| k-X0|,可以近似地使用如下的差异显着限度;Da(r—1,
k-X0|,可以近似地使用如下的差异显着限度;Da(r—1, nk-r)
nk-r)
(2)Tukey法,简称T法(1);S法:r个 k两两比较,并在此基础上进一步分组比较(线性对比)。这两种比较的差异显着限度分为nk≡n与nk不全相等两种情形,如表48—5所示:
k两两比较,并在此基础上进一步分组比较(线性对比)。这两种比较的差异显着限度分为nk≡n与nk不全相等两种情形,如表48—5所示:
表48—5 两两比较和线性对比的差异显着限度

表中的qα(f1,f2)与Sα(f1,f2)可以分别查“多重比较中的q表“和”多重比较中的S表”得到。f1,f2表示第一、第二自由度。可以看出,两两比较是线性对比在ck=1,ct=-1,而其他r-2个系数都等于0时的特例。
(3)多重极差检验法(Multiple-range test):有Duncan法(2)与S-N-K(Student-Newman-Keul)法两种。Duncan法查SSR表得SSRα(p,r(n-1));S-N-K法查“多重比较中的q表”得qα(p,r(n-1))。这两种分位数的第一自由度p表示大小在要比较差异显着性的Xk与 t之间,即不小于min{
t之间,即不小于min{ k,
k, t}、不大于max{
t}、不大于max{ k,
k, t}的平均数的个数,这p个平均数的极差是|
t}的平均数的个数,这p个平均数的极差是| k-
k- t|。p=2,3,……,r,这就是“多重极差”的含义。分别p=2,3,……,r,上述的p个平均数的极差|
t|。p=2,3,……,r,这就是“多重极差”的含义。分别p=2,3,……,r,上述的p个平均数的极差| k-Xt|的差异显着限度分别为:
k-Xt|的差异显着限度分别为: qα(p,r(n-1))
qα(p,r(n-1)) 。
。
以上两种多重极差检验法,在理论上只适用于nk≡n,k=1—r;如果nk不全相等,对于p个Xk的极差R= max—Xmin,可以近似地使用如下的差异显着限度:SSRα(p,
max—Xmin,可以近似地使用如下的差异显着限度:SSRα(p, nk—r)·
nk—r)·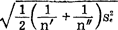 qα(p,
qα(p, nk-r)
nk-r) 其中n′和n″是这p个
其中n′和n″是这p个 k的最大值
k的最大值 max和最小值Xmin对应的样本容量。
max和最小值Xmin对应的样本容量。
需要说明,T法的每两个平均数之差的绝对值| k—
k— t|,1≤k<t≤r,就是S-N-K法的多重极差。这两种多重比较方法都查“多重比较中的q表”,它们之间的区别在于T法用于所有的“多重极差”的差异显着限度qα(r,r(n-1))
t|,1≤k<t≤r,就是S-N-K法的多重极差。这两种多重比较方法都查“多重比较中的q表”,它们之间的区别在于T法用于所有的“多重极差”的差异显着限度qα(r,r(n-1)) ,在S-N-K法中仅用于p=r对应的一个极差。由于qα(p,r(n-1))对于固定的r(n-1)随p=2,3,……,r增大而增大,因此除去p=r以外的差异显着限度,T法的都大于S-N-K法的。所以对于同一批Xk,k=1—r,|
,在S-N-K法中仅用于p=r对应的一个极差。由于qα(p,r(n-1))对于固定的r(n-1)随p=2,3,……,r增大而增大,因此除去p=r以外的差异显着限度,T法的都大于S-N-K法的。所以对于同一批Xk,k=1—r,| k-
k- t|,1≤K<t≤r之中超过差异显着限度者,S-N-K法的总是多于T法的。一般S-N-K法用于初级试验(例如增产新品种的大范围粗选),以免漏掉可能的显着差异;T法用于进一步试验(小范围精选用于推广的增产新品种),以免混进不显着差异。
t|,1≤K<t≤r之中超过差异显着限度者,S-N-K法的总是多于T法的。一般S-N-K法用于初级试验(例如增产新品种的大范围粗选),以免漏掉可能的显着差异;T法用于进一步试验(小范围精选用于推广的增产新品种),以免混进不显着差异。
不能不指出,有一种被称为LSD(LeaSt-significant difference,最小显着差数)的多重比较方法,从本世纪50年代以来不断地在国内外出版的生物统计书籍中被指出其理论上的缺陷,我国的大学数学系“概率论与数理统计”教材早在60年代初已经对此进行过分析。此后出版的一部分生物统计书籍继续介绍这种方法,同时告诫生物学家注意避免误用;但是也有极少数生物统计书籍在90年代初仍然不加分析地称其为“最常用的”两种多重比较方法(LSD法和LSR法)之一,甚至“最小显着差数法:此法适用于试验有对照的情况。……LSD法要求试验有对照,……”(3)事实上,在试验有对照的情形,作为“对照”的平均数X0将与其他的平均数分别进行比较:| k-X0|,k=1—r-1,从而多次被使用。这不是LSD法的要求,而恰恰被包括在LSD法的理论缺陷之内,是应该避免的对LSD法的误用。
k-X0|,k=1—r-1,从而多次被使用。这不是LSD法的要求,而恰恰被包括在LSD法的理论缺陷之内,是应该避免的对LSD法的误用。
(编者:刘长安 审者:孙尽善)