双因子方差分析
出处:按学科分类—农业科学 农业出版社《水产养殖手册》第905页(1196字)
对于在因子A的r1个水平Ak,k=1—r1和因子B的r2个水平Bt,t=1—r2全面搭配(组合)AkBt, 条件下产生的r1r2个相互独立的正态总体Xkt,
条件下产生的r1r2个相互独立的正态总体Xkt, ,双因子方差分析要解决的问题是以总体方差
,双因子方差分析要解决的问题是以总体方差 ,
, 为前提,对于因子A在因子B各水平均衡的条件下,以及因子B在因子A各水平均衡的条件下,推断μk·
为前提,对于因子A在因子B各水平均衡的条件下,以及因子B在因子A各水平均衡的条件下,推断μk·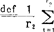 μkt,k=1—r1是否全相等(1);
μkt,k=1—r1是否全相等(1); ·
· 2是否全相等,并研究A与B的交互影响A×B(2)。
2是否全相等,并研究A与B的交互影响A×B(2)。
对于—组r1r2个样本观测值xkti, ,i=1—n,定义:
,i=1—n,定义:

对r1r2n个数据,定义总的平均数X与差异平方和SST:

下面研究SST的分解以及分解的各差异平方和的计算公式:

上式可以改写为

其中:

需要定义下列方差和F:
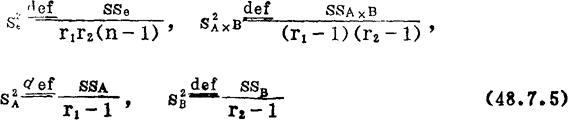

(48.7.6)式的计算步骤如表48—6(二)所示;表中(一)计算X2的公式是

上式括号外的系数是 (表48—6附文后)。
(表48—6附文后)。
表48—6 (一)计算X2;(二)计算FA×R、FA、FB

如果FA×B
需要指出,在样本容量n=1情形的双因子方差分析与正交设计的方差分析中,交互影响平方和常常被误认为是随机平方和,并且被称为误差平方和。对于多因子试验,首先是各因子的水平搭配设计:全面搭配或者正交搭配(两两全面搭配)。每一个水平搭配(以及单因子试验的每一个水平)称为一个“处理”;然后是“处理”的实施设计(例如,拉丁方设计)。以上所述是多因子实验设计的前后两个步骤。
(编者:刘长安 审者:孙尽善)