有溶液参与反应的热力学计算

出处：按学科分类—数理科学和化学 东北大学出版社《无机物热力学数据手册》第12页（4467字）

上节的计算实例都是在以拉乌尔定律为依据来处理溶液而得到的式(58)至式(72)的基础上进行的，各物质的标准态都是纯物质，计算时不涉及标准态的转换，但必须将浓度换算为摩尔分数。但实际应用中却很少使用摩尔分数，特别是涉及到溶质参与的化学平衡计算，经常使用质量百分浓度和其他浓度。这就出现了以亨利定律为依据来处理溶液，对标准态作适当转换的另一种计算方法。

1．以亨利定律为依据的溶质化学势表达式及其标准态

仿式(56)至(58)的处理方法，可得到溶质Bi服从亨利定律时的化学势为

式中c_i是B_i的浓度；由于c_i有单位，而取对数时不能带单位，所以引入c^θ。c^θ称为标准浓度，其数值为1，其单位与c_i的单位相同。例如c_i代表质量摩尔浓度m时，c^θ写成m^θ，其值为1mol·kg^－1；c_i代表体积摩尔浓度时，c^θ之值为1mol·dm^－3；当ci代表质量百分数(%i)或摩尔分数(x_i)时，由于这两种浓度都是无量纲的，c^θ的值为1。

B_i不服从亨利定律时，式(73)中的c_i／c^θ亦可用活度a_i代替，得到

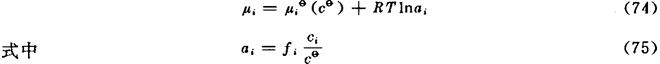
a_i是B_i的活度，f_i是B_i的活度系数。f_i＞1表示对亨利定律呈正偏差；f_i＜1则呈负偏差；f_i=1表示B_i服从亨利定律，这时a_i=c_i／c^θ。

式(74)和式(73)中的μ_i^θ(c^θ)是标准化学势。标准态就是c_i=1的服从亨利定律(f_i=1)的溶液。标准态的c_i和f_i均为1；标准态的活度值也为1。

由于c_i可以采用不同的浓度单位，故有不同的标准态。例如：

当浓度用摩尔分数x_i表示时，标准态就是将亨利定律直线延长到x_i=1处的假想状态。这时，式(75)写成

a_i=∫_ix_i (75a)

当浓度用质量百分数%_i表示时，标准态乃是亨利定律直线上浓度为1%的状态，也就是服从亨利定律的1%溶液(通常简称为1%溶液)。这时，式(75)写成

a_i=f_i〔%i〕 (75b)

当浓度用摩尔百分数mol%i表示时，标准态便是亨利定律直线上x_i=0．01处的状态，也就是服从亨利定律的x_i=0．01溶液。这时，式(75)写成

a_i=f_i〔mol%i〕 (75c)

当浓度用质量摩尔浓度表示时，标准态则是亨利定律直线上m_i=1的状态，也就是服从亨利定律的mi=1的溶液。这时，式(75)写成

以上四式中的a_i及f_i在数值上都是各不相同的。但当溶液变稀时，四式中的f_i值都趋于相同。这时f_i与γ_i的关系是

γ_i=γ_i^°f_i (76)

式中γ_i^°是以纯B_i为标准态含B_i无限稀时的活度系数，即

2．标准溶解自由能

恒温下，组元B_i溶解过程的标准吉布斯自由能变，称为B_i的标准溶解自由能，以△G_i^θ表之，即

B_i=〔B_i〕 △G_i^θ

△G_i^θ是〔B_i〕的标准化学势与纯B_i的化学势之差，其值与〔B_i〕的标准态有关：

1)当〔B_i〕的标准态是纯B_i时，△G_i^θ=0，〔B_i〕的活度用a_i=γ_ix_i计算。 即式(61)。

2)当〔B_i〕的标准态是将亨利定律直线延长到x_i=1的假想状态时，

B_i=〔B_i〕_x △G_i^θ=RT1nγ_i^o (78)

〔Bi〕的活度用a_i=f_ix_i计算，即式(75a)

3)当〔B_i〕的标准态是亨利定律直线上浓度为1mol%(即x_i=0．01)的溶液时，

〔B_i〕的活度用a_i=∫_i〔mol%i〕计算，即式(75c)。

4)当〔B_i〕的标准态是亨利定律直线上浓度为1%的溶液时，

式中Mi和M₁分别代表溶质B_i和溶剂B₁的摩尔质量。这时活度用式(75b)计算，即a_i=f_i〔%i〕，不必将〔%_i〕换算为x_i。所以，这种标准态在实际工作中得到广泛应用，但在计算△G^θ和K^θ时，要计入标准溶解自由能(参见下例)。

本书表3－2和表3－3中列出了1600℃的铁液和1200℃的铜液中某些溶质的标准溶解自由能(以1%溶液为标准态)。

〔计算实例〕 已知1873K的铁液中含钒为0．08%，采用1%溶液为标准态，计算下列反应的K^θ和平衡氧分压：

2〔V〕_%+3／2O₂=V₂O₃(s)

若po₂=101．3kPa，求反应的△G。

此例和上例(见11页)的条件相同，算法不同，但结果应相同。

由表2－3和表3－2查得：

对以上二反应作线性组合(1)－2(2)得

在T=1873K时，△G₃^θ=－545．7kJ·mol^－1

铁中含钒很低，可认为服从亨利定律，所以f_v=1，a_v=f_v〔%V〕=0．08

将K₃^θ=1．66×10¹⁵，a_v=0．08，a_v2o3=1代入上式，可求得p_o2／p^θ=2．07×10^－9

∴ p_o2=2．07×10^－9×101325=2．10×10^－4Pa

当p_o2=101．3kPa时

以上二例算出的平衡氧分压及△G均相同，但K^θ和AG^θ却不同。这是由于〔V〕标准态不同所造成的。

3．相互作用系数

设B₁代表溶剂，B₂，B₃，……，B_m代表各溶质，则当溶液较稀(x_i→1)时，溶质B_i的活度系数γ_i与浓度的关系是

ε_i^j称为溶质B_j对B_i的一阶相互作用系数；ε_iⁱ称为B_i自身的一阶相互作用系数。

当B_i的浓度用质量百分数时，对f_i亦有类似的关系：

e_i^j亦称为溶质B_j对B_i的一阶相互作用系数；ei1称为B_i自身的一阶作用系数。

本书表3－4和表3－5中列出了铁液中某些元素的一阶相互作用系数。若知道溶质的浓度，由表中查出相互作用系数后，便可依式(81)或式(82)求出活度系数。

〔计算实例〕 已知铁基合金中溶质的浓度为x_si=0．008，x_M0=0．01，x_cr=0．013。求在1873K及p_N2=101．3kPa下合金中平衡含氮量〔%N〕

首先求氮的活度系数f_N。由表3－4查得：，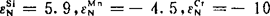

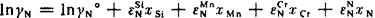
考虑到和x_N均甚小，上式最后一项可以忽略不计。代入上述数据，并应用式(76)，得

f_N=0．88

其次，求平衡的氮活度和氮浓度，查表3－2得

T=1873K时，△G^θ=48346J·mol^－1

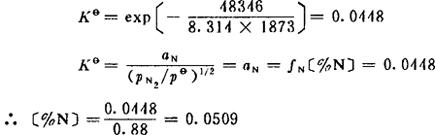
〔计算实例〕 用CaS作固体电解质构成电池测定铁液中的硫活度时，CaS会被铁液中的氧所氧化

CaS(s)+〔O〕=CaO(s)+〔S〕

已知铁液中含有0．65%C和0．052%S，求在1900K，铁液中允许的最大氧含量〔%O〕和氧活度是多少才不致发生上述反应。

首先，由表2－3中数据算得下反应的△G^O：

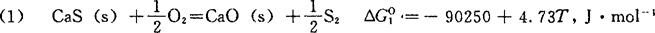
其次，由表3－2查得：

进行线性组合(1)－(2)+(3)得：

T=1900K时，△G₄^θ=－49165J·mol^－1

再由表3－5查得：，，，，。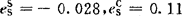

在反应(4)中，a_cas=1，a_cao=1，所以

取对数

lgK₄^θ=lgf_s+lg〔%S〕－lgfo－lg〔%O〕 (a)

上式中各项可以分别由已知数据求得：

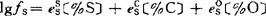=－0．028×0．052+0．11×0．65－0．27〔%O〕=0．070－0．27〔%O〕

l=－0．133×0．052－0．45×0．65－0．20〔%O〕=－0．299－0．20〔%O〕

将以上各项及〔%S〕=0．052代入式(a)，整理后得

lg〔%O〕+0．07〔%O〕=－2．266

解之得允许的最大(平衡)含氧量为

〔%O〕=0．0054

将此值代回lgf_o=－0．299－0．20〔%O〕中，求得f_o=0．501

∴ a_o=0．501×0．0054=0．0027