函数的连续性
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第40页(2941字)
连续的定义1 设函数f(x)在Uδ(x0)内有定义,如果当自变量的增量△x趋向于零时,对应的函数增量
△y=f(x0+△x)-f(x0)
也趋向于零,即
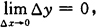
或

则称函数f(x)在点x0处连续,x0为f(x)的连续点.
连续的定义2 函数f(x)在点x0处满足:
(1)f(x)在点x0处有定义;
(2) 存在;
存在;
(3) .
.
则称函数f(x)在点x0处连续.
左连续 若函数f(x)在(x0-δ,x0]内有定义,且
f(x0-0)=f(x0),
则称f(x)在点x0处左连续.
右连续 若函数f(x)在[x0,x0+δ)内有定义,且
f(x0+0)=f(x0),
则称f(x)在点x0处右连续.
开区间内的连续函数定义 在开区间内(a,b)每一点都连续的函数,称为在该开区间(a,b)上的连续函数,或者说函数在该开区间(a,b)内连续.
闭区间上的连续函数定义 如果函数f(x)在开区间(a,b)内连续,在右端点b左连续,在左端点a右连续,则称函数f(x)在闭区间[a,b]上连续.
定理 函数f(x)在x0处连续 函数f(x)在x0处既左连续又右连续.
函数f(x)在x0处既左连续又右连续.
函数的间断点定义 函数f(x)在点x0的某去心邻域内有定义.如果函数f(x)有下列三种情况之一:
(1)f(x)在点x0处没有定义;
(2)在x=x0有定义,但 不存在;
不存在;
(3)在x=x0有定义,且 存在,但
存在,但 .
.
则称函数f(x)在点x0处间断,称点x0为f(x)的间断点.
第Ⅰ类间断点
1.跳跃间断点 如果函数f(x)在点x0处左、右极限都存在,但f(x0-0)≠f(x0+0),则称点x0为函数f(x)的跳跃间断点.
2.可去间断点 如果函数f(x)在点x0处左、右极限都存在,且 ,但x0是f(x)的间断点,则称点x0为函数f(x)的可去间断点.
,但x0是f(x)的间断点,则称点x0为函数f(x)的可去间断点.
第Ⅱ类间断点 如果函数f(x)在点x0处的左、右极限至少有一个不存在,则称点x0为函数f(x)的第二类间断点.
连续函数的和、积及商的连续性定理
(1)有限个在某点连续的函数的和是一个在该点连续的函数.
(2)有限个在某点连续的函数的乘积是一个在该点连续的函数.
(3)两个在某点连续的函数的商是一个在该点连续的函数,但要分母在该点不为零.
反函数连续性定理 严格单调的连续函数必有严格单调的连续反函数.
复合函数连续性定理 设函数u=φ(x)在点x=x0连续,且φ(x0)=u0,函数y=f(u)在点u=u0连续,那么复合函数y=f(φ(x))在点x=x0也是连续的.
基本初等函数在它们的定义域内都是连续的.
一切初等函数在其定义内的区间内都是连续的.
最大值和最小值定理
定义:若区间I上,存在点ξ,使在I上任何一点x均有f(ξ)≥f(x)(或f(ξ)≤f(x))则称f(ξ)为函数f(x)在区间I上的最大值(或最小值).
在闭区间上连续的函数在该区间上一定有最大值和最小值.
如果函数f(x)在闭区间[a,b]上连续,那么至少有一点ξ1∈[a,b],使f(ξ1)是f(x)在[a,b]上的最大值,至少有一点ξ2∈[a,b],使f(ξ2)是f(x)在[a,b]上的最小值(见图2.9).

图2.9
有界性定理 在闭区间上连续的函数一定在该区间上有界.
零点定理 设函数f(x)在闭区间[a,b]上连续,且f(a)与f(b)异号(即f(a)·f(b)<0),那么在开区间(a,b)内至少有函数f(x)的一个零点,即至少有一点ξ(a<ξ<b)使f(ξ)=0.
从几何上看,如果连续曲线y=f(x)的两个端点位于x轴的不同侧,那么这段曲线与x轴至少有一个交点(见图2.10).
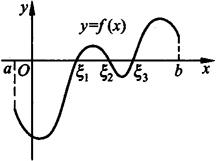
图2.10
介值定理 设函数f(x)在闭区间[a,b]上连续,f(a)=A,f(b)=B,且A≠B,那么,对于A与B之间的任意一个数C,在开区间(a,b)内至少有一点ξ,使得f(ξ)=C(a<ξ<b).
从几何上看,连续曲线y=f(x)与水平直线y=C至少有一个交点(见图2.11).

图2.11
推论 在闭区间上连续的函数必取得介于最大值M与最小值m之间的任何值.
一致连续的定义 设函数f(x)在区间I上有定义.如果对于任意给定的正数ε,总存在相应的正数δ,使得对于区间I上的任意两点x1,x2,当|x1-x2|<δ时,就有|f(x1)-f(x2)|<ε,那么称函数f(x)在区间I上是一致连续的.
一致连续性定理 如果函数f(x)在闭区间[a,b]上连续,那么它在该区间上一致连续.