线性子空间的定义
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第346页(2168字)
定义 S是数域F上的线性空间,W是S的非空子集,若W对S的两种运算(加法和数量乘法)仍构成一个线性空间,则W称为S的线性子空间.
W是S的子空间的充分必要条件 W是S的子空间的充分必要条件是线性空间S的非空子集W对于S的两种运算封闭,即W是S的子空间的充分必要条件是:
(1)W是非空集.
(2) ,则α+β∈W.
,则α+β∈W.
(3) ,则kα∈W.
,则kα∈W.
W是S的子空间的必要条件
(1)S的零向量0在W中.
(2)若 ,则-α∈W.
,则-α∈W.
(3) ,则
,则
k1α1+k2α2+…+krαr∈W.
平凡子空间 线性空间S本身是S的一个子空间.
由S的单个零向量组成的集合也是S的子空间,称为零子空间.
以上两个子空间称为平凡子空间,其余子空间称为非平凡子空间.
生成子空间 设α1,α2,…,αr是线性空间S的一组向量,它们的全部线性组合所成的集合非空,满足封闭性条件,故是S的子空间,称为由向量α1,α2,…,αr生成的子空间,记作
L(α1,α2,…,αr).
等价向量组生成相同的子空间 两个向量组生成相同的子空间的充分必要条件是两个向量组等价.
生成子空间的维数 生成子空间L(α1,α2,…;αr)的维数,等于向量组α1,α2,…,αr的秩r(α1,α2,…,αr).
子空间的交 设W1,W2都是数域F上的线性空间S的子空间,则W1,W2的公共元素的集合记作W1∩W2,即
W1∩W2={αlα∈W1且α∈W2},
则W1∩W2也是S的子空间,称为子空间W1,W2的交.
子空间的和 设W1,W2都是数域F上的线性空间S的子空间,则集合{α=α1+α2|α1∈W1,α2∈W2}也是S的子空间,记成
W1+W2={α=α1+α2|α1∈W1,α2∈W2},
称为子空间W1与W2的和.
维数公式 设W1,W2是线性空间S的子空间,则公式
dimW1+dimW2=dim(W1+W2)+dim(W1∩W2)
称为维数公式,且有以下关系:
(1)因 ,故
,故
dim(W1∩W2)≤dimW1,dim(W1∩W2)≤dimW2.
(2)因 ,
, ,故
,故
dimW1≤dim(W1+W2),dimW2≤dim(W1+W2).
(3)若dimW1+dimW2>dimS,则dim(W1∩W2)>0.
(4)W1∩W2是S中既包含在W1内,又包含在W2内的最大的子空间.
(5)W1+W2是S中的既包含W1又包含W2的最小的子空间.
子空间的直和 设W1,W2是线性空间S的两个子空间,如果W1+W2中的每个向量α可表示成
α=α1+α2(其中α1∈W1,α2∈W2),
且其表示法是惟一的,则称W1+W2为直和,记作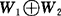 .
.
直和的充要条件 W1,W2是线性空间S的两个子空间,则
(1)W1+W2是直和 中的零向量可表示成
中的零向量可表示成
0=α1+α2(其中α1∈W1,α2∈W2),
其表示法是惟一的.
(2)W1+W2是直和
W1∩W2={0}.
(3)W1+W2是直和
dim(W1+W2)=dimW1+dimW2.