椭圆的参数方程

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第73页（760字）

(1)(a>b>0)的参数方程为

(2)(a>b>0)的参数方程为

例1 若椭圆mx²+y²=8与9x²+25y²=100的焦距相等，则实数m为＿＿．

例2 已知F₁为椭圆的左焦点，A、B分别为椭圆的右顶点和上顶点，P为椭圆上的点，当PF₁⊥F₁A，PO∥AB(O为椭圆中心)时，求椭圆离心率．

解 设椭圆方程为

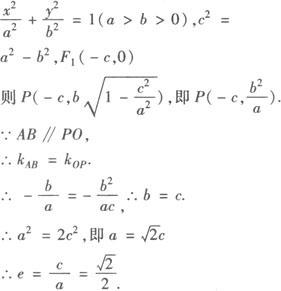
例3 CD是椭圆(a>b>0)长轴A₁A₂垂直的弦，求直线A₁C与A₂D交点M的轨迹方程．

策略 点M从动于C，也从动于D，而点C、D中有一个确定，另一个也相应确定，即点M从动于椭圆上的点C(或点D)，所以应以点C的坐标为参数，利用参数法求轨迹方程．

解 设C(acosθ，bsinθ)，则D(acosθ，—bsinθ)，

两式相乘得

即(y≠0)，即为动点M的轨迹方程．