丁巨算法

出处：按学科分类—文体、科学、教育 吉林大学出版社《四库大辞典下》第1749页（1238字）

八卷。

元丁巨(生卒年不详)撰。丁巨始末未详，在《丁巨算法》自序中，丁巨记载了成书经过：“独余幼贱，不伍时流，经籍之余事。法物度轨，则间尝用心。

因于算术上自九章，下至小法，数十百家，摘取要略。

述算法八卷。”《丁巨算法》今仅有残本面世，在《知不足斋丛书》中收录六十二问，不足一卷；在《永乐大典》卷一六三四三至卷一六三四四中收有提纲一条，另有二十七问。

其中提纲是列于问题前面的关于正方形与其内切圆、立方体与其内切球的有关周长、面积和体积等计算公式八条：“方求圆〔二十二乘，七除〕。圆求方〔七乘，二十二除〕。平面求周〔圆十二乘，方四乘〕。外圆求积〔圆物，六乘十二除〕。

〔方物，八乘十六除〕。立圆求径〔九乘，十六除〕。

立方求圆〔十六乘，九除〕。见斜求方〔五乘，七除〕。见方求斜〔七乘，五除〕。”现存的八十九个问题均是一般应用题，比较简单，只有一题为三元一次方程组应用题。大量的是度量衡换算的商业算题。例如：“今有鸡三只，价值二两；鸭七只，亦值二两。今持钱一百两，欲买二色各停，问鸡鸭各价多少?答曰：各买一百零五只。鸡价七十两，鸭价三十两。

以钞一百两，以二十一乘之得二千一百为实，以二十为法除之，得一百零五只，乃鸡鸭数也。

求价者倍鸡数三除之，倍鸭数七除之也。

”在书中丁巨已广泛使用了十进小数，他称小数为“省数”，在解释权衡单位进率“两”后说：“今从省数者，两下止言钱、分、厘、毫、丝、忽，如银钱法。犹田亩之不用里角，而从顷、分、厘、毫、丝、忽也。

”并且还给出了小数的专门记法，把“六十七两六钱八分”记作“⊥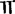⊥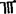”小数部分以小字记之，说明当时中国已相当熟练地使用十进小数了。丁巨在书中还用歌诀的形式给出一些问题的计算公式，如堆垛公式：“草垛添兴，以元乘今，折半积真；三角添一，又添二乘，六而一精，……”即为茭草垛：1+2+3十…+n=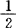n(n+1)；三角垛：1+3+6+…+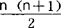=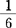n(n+1)(n+2)；……。

在书中丁巨十分重视总结一般性的算法。他将一类比例算题称为“两头交易”，并给出了一般方法。

例如“元雇车一两，议行道一千里，载重一千二百斤，与钞七十五两；今添重三百六十斤，行一千三百里，问与钞几何?”“此两头交易也，以今行道乘今载重，与元与钞相乘为实，却以元行道乘元载重为法，除之。如减斤重，减行道数，皆同此法，此双头交易乘除也”。对此类问题他进一步总结说：“凡两头交易，先布六草为法，己负者：甲乙乘为法，丁戊乘为实；丁怯者丙戊乘为法，甲乙己乘为实，戊阙者丙丁乘为法，甲乙己乘为实。甲乙丙，丁戊己，若以复乘之除之亦通。

”在筹算除法方面丁巨提出了“撞归法”，改善了筹算除法运算。总之，《丁巨算法》代表了元明之际我国商业数学的发展水平，说明了当时数学进一步实用化、大众化，起到了普及数学教育的作用。

《丁巨算法》成书于1355年，全帙版本不详，《永乐大典》中只有一小部分，鲍廷博的《知不足斋丛书》与李俨的《十三、十四世纪中国民间数学》中都录有残本。