光电角度读数装置

出处：按学科分类—工业技术 中国建材工业出版社《工程测量实用技术手册》第452页（4145字）

电子经纬仪的光电角度读数装置有编码度盘测角系统、光栅度盘测角系统、动态测角系统三种，现分别介绍如下。

1．编码度盘测角系统

编码度盘的每一个位置都可以读出度、分、秒的值。光学编码度盘(简称码盘)是以二进位制代码运算为基准的绝对值式的编码器，在度盘上刻有数道同心圆，等间隔地设置透光区域和不透光区域，由它们组成的分度圈称为码道。用透光和不透光两种状态代表二进制代码的“1”和“0”两个状态，里圈代表高位数，外圈代表低位数，如图18－61为4码道度盘，沿径向由里向外可读出4位二进制数，如图中顺时针方向依次可读出0000、0001、0010、…、1111，各区间的状态见表18－11。依据两区不同的状态，便可测出该区的夹角。

表18－11 电子度盘各区间的状态与编码

图18－61 编码度盘

读数系统原理如图18－62所示，在度盘半径方向的直线上，在每一码道设置两个接触片，一个为电源，另一个为输出。测角时，接触片固定，当度盘随照准部旋转到某个目标制动之后，接触片就和某一区间相接触，由于该区的导电或不导电，得到该区间的电信号状态。图中为1001，若照准部旋转到第二个目标，输出端状态为1101，则可知该角值为9～13区间的角度。

图18－62 读数系统

2．光栅度盘的测角系统

均匀地刻有许多等间隔狭缝的圆盘，称为光栅度盘。如图18－63所示，光栅的基本参数是刻线密度(每毫米的刻线条数)和栅距(相邻两栅之间的距离)。光栅的线条处为不透光区，缝隙处为透光区。在圆形光栅盘上下对应位置上装上照明器和光电接收管，将光栅的透光与不透光信号转变为电信号。当照明器和接收管随照准部相对于光栅盘移动，由计数器累计求得所移动的栅距数，即可求得所转动的角度值。该系统属于累计计数，通常称为增量式读数系统。

图18－63 光栅度盘

一般光栅的栅距已很小，例如，在80mm直径的度盘上刻有12500条刻线(刻线密度为50线／mm)，光栅距的分划值为1′44″，显然仍不能满足测角要求，为了提高测角精度，还必须将其放大，再进行细分。在光栅测角系统中采用莫尔条纹技术来解决这个问题。产生莫尔条纹的方法是：取一小块与光栅盘具有相同密度和栅距的光栅，称为指示光栅，将指示光栅与光栅盘以微小的间距重叠起来，并使其刻线互成一微小的夹角θ，当光栅盘与指示光栅之间相对运动时，就会出现放大的明暗交替的条纹(栅距由d放大到W)，如图18－64所示。

图18－64 光栅莫尔条纹

(1)光栅度盘静态测角原理

如图18－65所示，指示光栅和光栅读数头与照准部固连在一起，进行测角时，主光栅盘不动，照准部连同指示光栅和光栅读数头相对于主光栅移动。欲测OB与OA方向的夹角，开机后瞄准A目标，照准部开始旋转时，指示光栅相对于主光栅盘每移过一个栅距W，即转过一个栅角，光探器上就掠过一个莫尔条纹，输出一个正弦信号；经过整形电路形成一个计数脉冲，直到瞄准B目标为止，电子计数器累计出指示光栅相对于主光栅移过的整栅角数φ₀的值，则该角度为φ=n·φ₀+△_φ，△_φ为不足一个栅角的尾数，用电子细分的方法求得。

图18－65 指示光栅和光栅读数头

光栅动态测角系统如图18－66所示，度盘圆周经向刻有1024条刻线，刻线栅角为φ₀=360°／1024。在光栅盘的外边缘对径处设置了一对与基座或支架固连的固定光栅L_S。对水平盘来说，L_S相当于零位置；对竖盘来说，L_S相当于竖盘指标线。在光栅盘的内边缘处，设置了一对与照准部固连的活动光栅L_R。L_S和L_R均由发光二极管和光控器组成。

图18－66 光栅动态测角系统

测角时，光栅盘由电动机驱动绕中心轴作匀速旋转，计取通过两个指标光栅间的分划信息通过粗测与精测而求得测角值。

1)粗测

即求出L_S的莫尔条纹个数N。在度盘同一径向的外边缘上设有两个标记a和b，度盘旋转时，以标记a通过L_a时起，记数器开始记取整间隙φ₀的莫尔条纹个数，当另一标记b通过L_R时记数器停止记数，此时记数器所得到的数值即为φ₀的莫尔条纹个数N。

2)精测

测角精度取决于精测的精度。精测即求出不满一个φ₀的尾值△_φ，通过光栅L_S和L_R产生两个信号S和R，△_φ可由S和R的相位差求得。精测开始后，当某一分划通过L_S时开始精测计数，计取通过的计数脉冲个数，一个脉冲代表一定的角度值(如2″)，而另一个分划通过L_R时停止计数。由计数器累计的数值求得△_φ的值，度盘旋转一周可测得1024个△_φ，然后取其平均值作为最终的△_φ值，最后求得角值：φ=N_φ0+△_φ。

(2)电子细分方法

在利用光栅度盘测角时，要使最小读数达到1″或0．1″，这就意味着要在度盘的圆周上刻划百万根甚至千万根条纹线，而在目前工艺上，这是极其困难的，甚至是不可能实现的。为了达到测角所需要的精度，且满足工艺上可能、经济上合理的要求，常采用电子细分技术。常用的电子细分方法有直接细分法、幅值分割细分法、移相细分法及调制细分法四种。这几种细分法可单独使用，也可将两种方法组合使用。电子经纬仪中常用直接细分法和调制细分法，现介绍如下。

1)四倍频直接细分法

在相当于度盘正弦光迹缝隙或莫尔条纹的一个周期内，彼此相隔90°相角(即四分之一周期)设置4个条形光探测器，如图18－67所示。由于每个光探测器所对应的光迹或莫尔条纹的位置不同，受光的面积也不同，故输出的信号大小也不同。设与第一只光探测器中心相对的正弦光迹的起始相位为0°，则4个光探测器中的电信号分别为：

图18－67 四倍频直接细分法

(a)正弦光迹与条形光二极管；(b)内插所用光电流

为了消除直流分量U₀和放大所得到的4个信号，可以利用差分放大电路来实现。通过图18－68所示的网路，可得到如下4个信号：

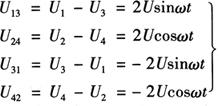
图18－68 差分放大电路

通过零鉴别器将4个交变信号整形为方波信号，该方波信号一方面经微分输出尖脉冲用于细分计数，另一方面用作正逆转向时的判向信号。

在一周期内正弦信号有4个过零点，可形成4个计数脉冲。即每通过一个正弦光迹或莫尔条纹可记录4个脉冲，故称四频倍。在该法中，光电信号经整形后直接产生计数脉冲，中间不再提取测微信息，故称为直接细分法，总称四倍频直接细分法。

2)调制细分法

直接细分法由于细分数少，只适用于中等精度的电子经纬仪。当要求测角最小分辨率达到1″或0．1″时，通常采用细分数可达1000的调制细分法。和直接细分法相似，调制细分法也是在正弦光迹缝隙或莫尔条纹的一个周期内，彼此相隔90°相角设置4个条形光探测器，如图18－68所示。由于各探测器相对正弦光迹或莫尔条纹的位置不同，受光的面积不同，产生的电流也不同。设第一只光探测器中线相对于正弦波的起时相位为φ，则各光探测器输出的电流为：

通过差分电路消去直流分量I₀，则得：

当照明光迹缝隙的光源以交流电馈电时，则I为时间t的函数，即：

I=I(t)=Isinωt

于是上一公式组现可写成：

(I₁－I₃)=2Isinφsinωt

(I₂－I₄)=2Icosφsinωt

将(I₁－I₃)相对于(I₂－I₄)移相90°，则有：

(I₁－I₃)=2Isinφcosωt

通过运算放大器将两信号(I₁－I₃)与(I₂－I₄)合成，则得合成信号I_t为：

I_t=2Isin(ωt+φ)

这样就把角位置的相位φ变成时间信号I_t的相位了。将此信号与调制信号Isinωt在检相器中比相，用填充计数脉冲法即可求得φ的大小，该过程可借用仪器中的相位计来完成。当相位计具有0．36°的分辨率时，细分数可达1000。