线性规划

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第267页（991字）

虽然大量的优化设计是非线性的，但由于目前对非线性规化还没有一个普遍适用的求解方法，而且解决非线性问题也大都离不开求解线性规化的方法。所以，讨论线性规化的求解方法是需要掌握的。为叙述方便，现例举某产品结构优化予以简单介绍。

某工厂生产A、B两种产品，并已知生产一件A产品所需甲、乙设备的生产时间分别为2小时和3小时，其利润为400元。而生产一件B产品则需甲、乙设备的生产时间分别为4小时和2小时，利润为600元。现每月可用于生产A、B产品的甲、乙设备生产时间分别为180小时及150小时，试问，如何制定A、B产品的生产计划才能在现在条件下获得最大利润?

若设A、B两种产品的生产量分别为X₁、X₂件，则可建立下述模型，即求一组非负的设计变量X₁、X₂，满足约束条件

2X₁+4X₂≤180

3X₁+2X₂≤150

X₁≥0，X₂≥0

使目标函数f(x)=400x₁+600x₂为最大。

对于这种只有两个设计变量的线性规划，可采用图解时方法进行求解。如图2．2．5－1，其中阴影部分是所有满足条件的设计方案的集合(称为可行域)，目标函数等值线的增长方向为箭头所示方向。显然，P点是可行域内使目标函数取值最大的点，即为所求的最优设计方案，并由此得最优解为生产A产品30件，B产品30件，得最大利润为3万元。

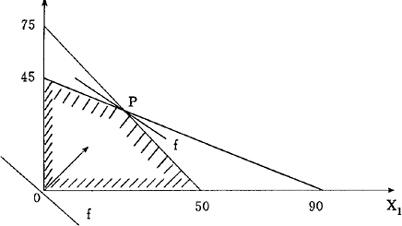
图2．2．5－1

由图解法不难看出，满足线性规划约束条件的所有设计方案的集合，构成一凸多边形或凸多面体(凸集)，最优解一般都在它们的顶点(极点)处得到，由此而产生求解一般线性规划的单纯形法。因此，单纯形法的基本思想，是先找一位于顶点上的解，并判断它是否为最优。若为最优便停止运算，否则应将它换算成另一顶点解，并使目标函数有所改善。如此重复上述过程，即可在有限步内获得最优解。

求解线牲规划问题的方法，除单纯形法外，还有对偶单纯形法、改进单纯形法以及求解运输作业法和求解整数解的整数规划法等。