动态分析法

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第673页（5352字）

动态分析法是在考虑资金时间价值的基础上，根据方案在研究期内的现金流量对其经济效益进行分析、计算、评价的一种方法。

动态分析法一般可分为现值法、年值法、内部收益率法及动态投资回收期法。

1．现值法

现值法的特点是使各备选方案在研究期中的现金流量现值化，并在此基础上选择最优方案。

现值法又可分为净现值法、净现值率法和现值成本法。

(1)净现值法(NPV法)

净现值法是分别把各方案在研究期内不同点上发生的所有现金流量按某一预定的折现率换算成等值的现值之和，然后比较各方案的现值和，其数值最大的方案就是最优方案。

上述的现值和应是所有现金流入量的现值和与所有现金流出的量的现值和之差，它被称为净现值，用符号NPV表示，其计算公式如下：

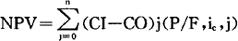
式中，n——方案的研究期；

i_c——基准收益率；

CI——现金流入量；

CO——现金流出量；

(CI-CO)₁——第j年的净现金流量。

净现值(NPV)大于零，说明方案能取得所希望的投资收益。因而NPV大于零的方案是可行方案。在若干个可行的备选方案中，NPV值最大的方案最优。

要说明的是，净现值指标有财务净现值指标、经济净现值指标等。财务净现值指标用于项目的财务评价，经济净现值指标用于国民经济评价。计算财务净现值指标时，各年的净现金流量按部门或行业的基准收益率折现，若尚未制定出基准收益率，则可按设定的折现率折现；计算经济净现值是用社会折现率进行折现。在介绍技术经济分析基本方法时，均以进行财务评价为例，故净现值计算式中也是用的基准收益率。

净现值法的计算步骤可简单地归纳如下：

①选定折现率。财务评价时，若已制定了部门或行业的基准收益率(i_c)则按部门或行业规定计算；若没有规定，则可根据项目追求的投资效果选定一个目标收益率(又称基准折现率)，选定这－目标收益率的基本原则是：不论是用银行贷款，还是用自筹资金进行投资，目标收益率均应高于贷款利率。根据国外经验，考虑到风险性等因素，目标收益率以在贷款利率的基础上再加5%为宜。例如，贷款利率为8%，则目标收益率应为13%。

若进行国民经济评价，计算经济净现值时，应采用国家统一制定和颁布的并定期进行调整的社会折现率(is)。

②画出项目在整个研究期内的现金流量图。

③将研究期发生的所有净现金流量按基准收益率折成现值，并将各现值进行代数运算，求出净现值(NPV)。

④方案比选。所有净现值大于零的方案都参加比选，对应于最大净现值的方案为最优方案。

如果方案在使用期内现金流量是年金序列，则根据年金现值公式求得现值：

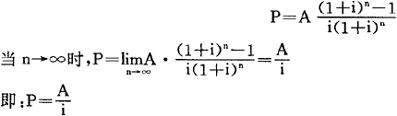
是无限长期限内的年金现值公式。

对于不同使用寿命期的对比方案，如各方案使用寿命相差不大但最小公倍数很大时，可以用公式来处理。

应用净现值法，克服了静态分析方法的缺陷。净现值法考虑了资金的时间价值以及投资项目在整个寿命周期内的费用和收益。

当两个方案投资额相差很大时，仅以净现值的大小来决定方案的取舍可能会导致错误的选择。

为了解决这一问题，就需引入净现值率。

(2)净现值率法

净现值率(又称为现值指数)法是在净现值法的基础上发展起来的，可以作为净现值法的一种补充。

净现值率是方案的净现值与投资现值之比，它反映了单位投资现值获得的净现值，其计算公式为：

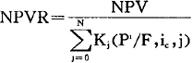
式中，NPVR——净现值率。

净现值率反映了方案的相对经济效益，净现值率愈大，投资的经济效益就越好。当用净现值率来选优时，应选净现值率最高的方案。只有在净现值率大于或等于零时，方案才是可行的。

当分别用NPV法和用NPVR法判别的最优方案结果相互间有矛盾时，最终确定的最优方案应视其具体情况而定。一般把NPVR作为辅助指标，但当各方案投资额悬殊很大或资金缺乏时，用NPVR法确定最优方案更恰当一些。

(3)现值成本法

应用净现值法、净现值率法来评价方案时，其前提是方案的每年收入能直接计算。当项目的几个备选方案的收入相同或无法计算项目收入但其各方案效果均相同时，只需比较方案费用就能择优。下面具体介绍这一方法——现值成本法。

现值成本法的本质与净现值法是相同的，其做法是把各方案在研究期内发生的所有费用均换算成现值之和(该现值之和称为现值成本，用符号Pc表示)，其数值最低的方案为最优方案，表达式为：

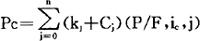
式中，P_c——现值成本；

Cj——第j年的经营成本。

2．年值法

年值法的要点是使各备选方案在研究期中的现金流量年金化，即以年(金)值为准，对所发生的现金流入和流出进行等价可比化并选择最优方案。

用年值法评价多个备选方案时，如果各方案的使用寿命相同，则研究期取寿命期；如果各方案的使用寿命不同，则仍要作与现值法相同的假设。第一，研究期必须是各对比方案寿命的最小公倍数或研究期无限长；第二，各方案在研究期内分别以相同规模重复投资多次。这两个假设的目的仍是要保证各方案具有相同的研究期，解决方案可比性问题。但是，年值法在实际计算时不必考虑研究期中方案重复投资的次数以及研究周期中的现金流量，而只要根据各方案在各自第一个使用寿命周期的年值即可进行比较选优。这是因为方案重复投资后的任意一个寿命期的年值与第一个寿命期的年值是相等的，也就是说，方案在整个研究期中的年值与第一个寿命期的年值相等。这样，比较不同方案的整个研究期的年值与比较各方案在第一个寿命期的年值的结果是相同的。

由于方案在研究期内的年值与重复投资的次数无关，因此，用年值法评价寿命期不同的方案时，可以直接计算方案在寿命期内的年值并加以比较。故年值法在这一点上比现值法要方便得多，这是年值法的优点。

把方案全部现金流量折算为年值之和，该年值之和称为净年值，用符号NAV表示。方案的净年值NAV大于零才能称为可行方案，在多个方案中，NAV值最大的方案最优。

如果净收益已经以年度量形式出现，投资为一次性投资Ko，残值为K_L，则净年值NAV为

NAV=－K_o(A／P，I_c，N)+M+K_L(A／F，i_c，n)

对于一般形式：

NAV=(NPV)·(A／P，i_c，n)

式中NPV为净现值。即首先将不规则的现金流量折算为净现值，然后利用资金回收公式转换成净年值。

但在不同情况下，用不同的方法其繁简程度相差很大。因此，要根据具体情况有选择地采用现值法或年值法。

表2．3．1－1列出了不同情况下宜采用的方法。

表2．3．2－1

3．内部收益率法

内部收益率法又称为内部报酬率法。

使方案在研究期内净现值为零时的折现率称为该方案的内部收益率，即公式

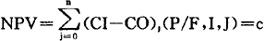
成立时所对应的i就是方案的内部收益率，通常用符号IRR表示。

用内部收益率法选择最优方案的基本步骤如下：

第一，将各方案按初始投资费用由小到大排列。

第二，计算第一方案内部收益率IRR(1)，判断其是否可行(即IRR(1)是否大于i_c)，如不可行，淘汰第一方案，再计算IRR(2)，判断第二方案可行否，如仍不可行，再依次下去，直到找出一个可行的方案为止。

第三，计算可行方案和后一个方案间的追加投资收益率为i^#，如i^*＞i保留投资大的方案，淘汰投资小的方案；反之则保留投资小的方案，淘汰投资大的方案。

第四，将保留的方案再按第三步的方法与后一个方案进行比较，依次比较下去，直到最后一个方案。最终未被淘汰的方案，就是最优方案。

在特定的条件下，内部收益率的解并非只是唯一的。

要说明的是现实经济活动中仅在极少数情况下会出现内部收益率有多解的现象。

4．动态投资回收期法

投资回收期反映了投资费用得到补偿所需的时间。作为投资者，理所当然地会非常关心投资回收期。通常，投资回收期愈短，投资风险就越小。这是因为方案中大多数数据来自预测、估计，预测的时间愈长，准确性就愈差。而且，收回投资后还可以进行新的投资。因此，投资回收期是决策的重要依据之一。为了弥补静态投资回收期的缺陷，现引入动态投资回收期的概念。

动态投资回收期是指在考虑了资金时间价值的情况下，从初始投资起到累计获得的净收益收回全部投资为止所需的时间。

如果项目为一次性投资，并且当年投产，每年获得的净收益均相等，则根据资金回收公式，并经整理后可得：

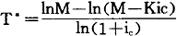
式中：T^*——动态投资回收期。

从公式中可看出：如果年净收益M为负或M≤Ki_c，对数没有意义，也就是说，投资无法实现回收。

公式仅适用于一次性投资且每年净收益相等的情况，但也可以用于不符合上述条件的大型项目的粗略估算。求解一般情况下的动态投资回收期用如下公式：

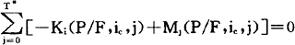
动态投资回收期虽然反映了投资回收的时间，但未能反映方案在整个寿命期的盈利情况。因此，它只能被广泛地用作辅助指标。当几种评价方法出现矛盾时，一般可以净现值法的结论为依据，只有在资金特别紧缺、投资风险很大的情况下，才把动态投资回收期作为评价方案最主要的依据之一。