交流信号及其幅度量值的表示
出处:按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第360页(3026字)
1.交变信号与正弦信号
无线电计量中研究或使用的信号绝大多数为交流信号,即其大小和方向随时间改变的信号。如大小随时间而改变,方向不随时间改变的信号为脉动信号;而大小和方向都随时间而改变的信号为交变信号。经过一定的时间T,信号的变化完成一个循环,以后随时间重复原来变化规律的信号,称为周期性交变信号。该信号重复一次的时间称为周期T,周期的倒数称为频率f,即单位时间内变化的次数,单位为赫兹。
按正弦函数变化的周期性交变信号称为正弦信号,可以表示为:
u=Umcos(ωt+ψ) (7.2-1)
式中u——正弦信号的瞬时值,即某一时间t的数值(包括大小和方向);Um——最大值幅度;ω——角频率,每秒钟变化的弧度,单位是弧度/秒,且有ω=2π/T=2πf;(ωt+ψ)——衡量随时间变化的进程的量,称为相位或相角;ψ——初相角,其大小取决于所选取的初始时间。
2.交变信号的幅度量值
在实际应用中,由于信号的波形不一,因此信号幅度量值的表示方法有多种,在计量测试时必须弄清被测对象的定义,否则会带来误差或导致错误的测量结果。
(1)瞬时值 交变信号u(t)在某一瞬间的值,称为该时刻的瞬时值。
(2)峰值 交变信号u(t)在一个周期内达到的最大值称为峰值,以Um表示。峰值又分为正峰值Um+和负峰值Um-。
(3)平均值 交变信号u(t)在一个周期内的平均值,即:

当u(t)含直流分量U0时,平均值];当u(t)不含直流分量时,平均值 。为了便于实际研究,以全波平均值作为平均值。
。为了便于实际研究,以全波平均值作为平均值。
1)全波平均值 交变信号u(t)的绝对值在一个周期内的平均值,即

2)正半波平均值 交变信号u(t)在正半周内的平均值,即:

3)负半波平均值 交变信号u(t)在负半周内的平均值,即

对于正弦信号,平均值是峰值的2/π(≈0.637)倍;对于方波, 。
。
(4)有效值 交变信号u(t)在一个周期内的均方根值称为有效值,以U表示,即:

有效值的物理意义是,该交变信号在时间T内在纯电阻上所产生的热量,与同样时间内加于同一负载产生同样热量的直流信号相等的数值。有效值能直接反映出交流信号能量的大小,在无线电计量测试中应用很广泛。除应用于电压计量外,对功率、噪声、失真度、频谱纯度以及能量转换等是十分重要的。另外,有效值具有简单的叠加性,便于计算。例如,当n个交变信号
u(t)=u1(t)+u2(t)+…+un(t) (7.2-7)
同时作用到一个电阻R上时,合成的总有效值为:

叠加性不适用于峰值和平均值,因为若干个交变信号的合成峰值或平均值不仅取决于每个信号分量的大小,而且还要考虑它们之间的相位关系。
对于正弦信号,有效值是峰值的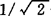 倍;对于方波,有效值等于峰值。
倍;对于方波,有效值等于峰值。
3.各种量值之间的关系
(1)波形因数 交变信号的有效值与平均值之比称为波形因数,即:

对于正弦信号,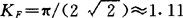 ;对于方波,KF=1。
;对于方波,KF=1。
(2)波峰因数 交变信号的峰值与有效值之比称为波峰因数,即:

对于正弦信号, ;对于方波,Km=1。
;对于方波,Km=1。
(3)中和因数 交变信号的峰值与平均值之比称为中和因数,即:

对于正弦信号,Ka=π/2≈1.57,对于方波,Ka=1。
上述的波形因数、波峰因数和中和因数充分反映出交变信号的峰值、平均值和有效值之间的相互关系,对于量值之间的换算有重要意义。
【参考文献】:
[1]王立吉、金国钧编着,高频电压的计量测试,计量出版社,1986。
[2]李世雄、彭幼伯等编着,低频电压的计量测试,计量出版社,1988。
[3]冯新善、吴幼璋等编着,高频、微波功率的计量测试,计量出版社,1987。
[4]张关汉、李光仪等编着,高频集总参数阻抗的计量测试,计量出版社,1986。
[5]胡希平、李湘编着,微波阻抗与反射的计量测试,计量出版社,1988。
[6]蔡新泉、关志仁等编着,高频、微波噪声的计量测试,计量出版社,1988。
[7]郭允晟、苏秉炜等编着,脉冲参数与时域测量技术,计量出版社,1989。
[8]吴毅、都世民等编着,高频、微波场强和干扰的计量测试,计量出版社,1986。
[9]谢上次、徐燕清编着,高频、微波相移的计量测试,计量出版社,1992。
[10]艾明、吴达慎等编着,失真与调制参数的计量测试,计量出版社,1989。
[11]黄福芸等主编,计量知识手册,中国林业出版社,1986。
[12]陈国瑞、华荣喜等编,工程电磁场与电磁波,西北工业大学出版社,1990。
[13]Ghose,R.N.,Microwave Circuit Theory and Analysis,McGraw-Hill Book Company,Inc.,1963。