无界函数的广义积分的审敛法
书籍:数学手册(大学生用)
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第98页(794字)
比较审敛法 设函数f(x)在区间(a,b]上连续,且

如果存在常数M>0及q<1,使得

则广义积分 收敛.
收敛.
如果存在常数N>0及q≥1,使得

则广义积分 发散.
发散.
极限审敛法 设函数f(x)在区间(a,b]上连续,且
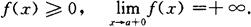
如果存在常数0<q<1,使得

则广义积分 收敛;
收敛;
如果存在常数q≥1,使得
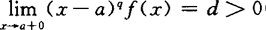 (或
(或 ),则广义积分
),则广义积分 发散.
发散.
Γ函数定义 .
.
Γ函数性质
(1)递推公式:Γ(s+1)=sΓ(s) (s>0).
(2)当s→+0时,Γ(s)→+∞.
(3)余元公式:
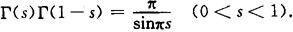
特别地,当 时,有
时,有
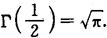
上一篇:函数的连续性
下一篇:数学手册(大学生用)目录