几何应用
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第105页(2220字)
平面图形的面积
1.直角坐标系情形
由曲线y=f(x)(f(x)≥0)及直线x=a,x=b(a<b)与x轴所围成的曲边梯形的面积A是定积分

其中被积表达式f(x)dx是面积元素(见图7.3).
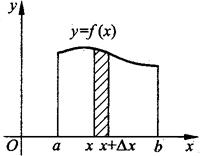
图7.3
2.曲边为参数方程的情形
当曲边梯形的曲边y=f(x)(f(x)≥0,x∈[a,b])由参数方程

给出时,曲边梯形的面积为

其中t1和t2对应曲线起点与终点的参数值.在[t1,t2](或[t2,t1])上x=φ(t)具有连续导数,y=ψ(t)连续.
3.极坐标系情形
设由曲线r=r(θ)及射线θ=α,θ=β围成一曲边扇形,求其面积.这里r(θ)在[α,β]上连续,且r(θ)≥0(见图7.4).

图7.4
面积元素为

曲边扇形的面积为
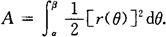
体积
1.旋转体
由一个平面图形绕这平面内一条直线旋转而成的立体,这条直线叫做旋转轴.
2.旋转体体积
求由连续曲线y=f(x),直线x=a,x=b及x轴所围成的曲边梯形绕x轴旋转而成的旋转体体积(见图7.5).
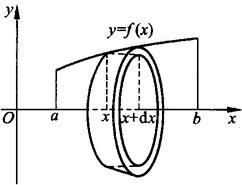
图7.5
取以dx为底的窄曲边梯形绕x轴旋转而成的薄片的体积为体积元素
dV=π[f(x)]2dx,
旋转体体积为

3.平行截面面积为已知的立体的体积
如果一个立体不是旋转体,但却知道该立体上垂直于一定轴的各个截面面积A(x),求这个立体的体积(见图7.6).

图7.6
过点x且垂直于x轴的截面面积A(x)为x的已知连续函数,体积元素为
dV=A(x)dx,
立体体积为

平面曲线的弧长
1.平面曲线弧长的概念
设A,B是曲线弧上的两个端点,在弧上插入分点A=M0,M1,…,Mi,…Mn-1,Mn=B,并依次连接相邻分点得一内接折线,当分点的数目无限增加且每个小弧段都缩向一点时,此折线的长 |的极限存在,则称此极限为曲线弧AB的弧长(见图7.7).
|的极限存在,则称此极限为曲线弧AB的弧长(见图7.7).

图7.7
2.直角坐标情形下平面曲线弧长公式
曲线弧为y=f(x)(a≤x≤b),f(x)在(a,b)上具有一阶连续导数,弧长元素为

弧长为
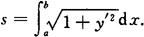
3.参数方程情形下平面曲线弧长公式
曲线弧为

其中φ(t),ψ(t)在[α,β]上具有连续导数,弧长元素为

弧长为

4.极坐标情形下平面曲线弧长公式
曲线弧为
r=r(θ) (α≤θ≤β),
其中r(θ)在[α,β]上具有连续导数,弧长元素为

弧长为
