空间曲面与曲线
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第126页(1613字)
球面方程
(1)球心为(x0,y0,z0),半径为R的球面方程为
(x-x0)2+(y-y0)2+(z-z0)2=R2.
(2)球心为原点,半径为R的球面方程为
x2+y2+z2=R2.
(3)球心在x轴上(R,0,0),半径为R的球面方程(即与Oyz坐标面相切于原点)为
x2+y2+z2=2Rx.
(4)球心在y轴上(0,0,R),半径为R的球面方程(即与Oxy坐标面相切于原点)为
x2+y2+z2=2Rz.
母线平行坐标轴的柱面方程
(1)柱面定义:在Oxy坐标面上的曲线L的方程为f(x,y)=0称为柱面的准线,过准线且平行z轴的所有直线所形成的曲面称为柱面.这些直线称为柱面的母线.柱面方程为
f(x,y)=0.
(2)设准线在yOz坐标面上的方程为f(y,z)=0,则母线平行x轴的柱面方程为
f(y,z)=0.
(3)设准线在Oxz坐标面上的方程为f(x,z)=0,则母线平行y轴的柱面方程为
f(x,z)=0.
椭球面方程(见图8.6) (a,b,c为正常数).
(a,b,c为正常数).

图8.6 椭球面: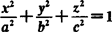
单叶双曲面方程(见图8.7)

图8.7 单叶双曲面

双叶双曲面方程(见图8.8)
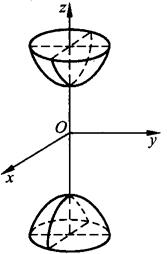
图8.8 双叶双曲面

椭圆抛物面方程(见图8.9)

图8.9 椭圆抛物面


双曲抛物面方程(见图8.10)

图8.10 双曲抛物面

投影柱面定义 过空间曲线C上每一点作平行坐标轴的直线.这些直线所形成的面称为投影柱面.设空间曲线C的方程为
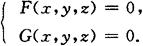
消去一个变量如消去z得方程
H(x,y)=0,
此方程即为投影柱面.
投影曲线定义 投影柱面(如H(x,y)=0)与坐标面(Oxy坐标面)的交线叫做曲线C在坐标面上(Oxy平面上)的投影曲线,简称为投影.