微分法在几何上的应用
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第149页(3134字)
空间曲线的切线与法平面方程
切向量 曲线上点M处切线的方向向量称为曲线的切向量(见图9.3).
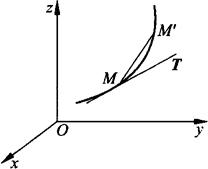
图9.3
法平面 过曲线上的点M且与切线垂直的平面称为法平面.
(1)设空间曲线的方程为

曲线在M处的切线方程为

切向量为T={φ′(t0),ψ′(t0),ω′(t0)}.曲线在M处的法平面方程为
φ′(t0)(x-x0)+ψ′(t0)(y-y0)+ω′(t0)(z-z0)=0.
(2)设空间曲线方程为

在点M(x0,y0,z0)处的切线方程为

切向量为T={1,φ′(x0),ψ′(x0)}.曲线在M处的法平面方程为
(x-x0)+φ′(x0)(y-y0)+ψ′(x0)(z-z0)=0.
(3)空间曲线方程为

曲线在M处的切线方程为

曲线在M处的法平面方程为

空间曲面的切平面与法线方程
法线 通过点M(x0,y0,z0)而垂直于切平面的直线称为曲面在该点的法线.
法向量 垂直于曲面上切平面的向量称为曲面的法向量(见图9.4).

图9.4
(1)设空间曲面的方程为F(x,y,z)=0,曲面在点M处的切平面方程为
Fx(x0,y0,z0)(x-x0)+Fy(x0,y0,z0)×(y-y0)+Fz(x0,y0,z0)(z-z0)=0.
曲面在点M处的法线方程为

曲面在M处的法向量为
n={Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0)}.
(2)空间曲面的方程为z=f(x,y),曲面在点M处的切平面方程为
fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0)=z-z0.
曲面在M处的法线方程为

方向余弦 若α,β,γ表示曲面法向量的方向角,并假定法向量的方向是向上的,即使得它与z轴的正向所成的角γ是锐角,则法向量的方向余弦为
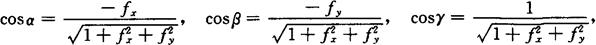
其中
fx=fx(x0,y0),fy=fy(x0,y0).
方向导数 函数的增量f(x+△x,y+△y)-f(x,y)与PP′两点间的距离 之比值,当P′沿着l趋于P时,如果此比的极限存在(如图9.5),则称这极限为函数在点P沿方向l的方向导数,记为
之比值,当P′沿着l趋于P时,如果此比的极限存在(如图9.5),则称这极限为函数在点P沿方向l的方向导数,记为

图9.5
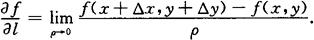
特别地,函数f(x,y)在点P沿着x轴正向e1={1,0}、y轴正向e2={0,1}的方向导数分别为fx,fy;沿着x轴负向、y轴负向的方向导数是-fx,-fy.
对于三元函数u=f(x,y,z),它在空间一点P(x,y,z)沿着方向L的方向导数,可定义为

其中
定理 如果函数z=f(x,y)在点P(x,y)是可微分的,那么函数在该点沿任意方向l的方向导数都存在,且有

其中φ为x轴到方向l的转角.
如果函数u=f(x,y,z)在点P(x,y,z)是可微分的,那么函数在该点沿任意方向l的方向导数都存在,且有
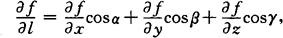
其中方向l的方向角为α,β,γ.
梯度 设函数z=f(x,y)在平面区域D内具有一阶连续偏导数,则对于每一点P(x,y)∈D,都可定出一个向量 这向量称为函数z=f(x,y)在点P(x,y)的梯度,记为
这向量称为函数z=f(x,y)在点P(x,y)的梯度,记为

函数在某点的梯度的方向与取得最大方向导数的方向一致,它的模为方向导数的最大值,即

当 不为零时,x轴到梯度的转角的正切为
不为零时,x轴到梯度的转角的正切为

设函数u=f(x,y,z)在空间区域G内具有一阶连续偏导数,则对于每一点P(x,y,z)∈G,梯度

等高线 曲线

称为函数z=f(x,y)的等高线.
梯度与等高线的关系 函数z=f(x,y)在点P(x,y)的梯度的方向与点P的等高线f(x,y)=c在这点的法线的一个方向相同,且从数值较低的等高线指向数值较高的等高线,而梯度的模等于函数在这个法线方向的方向导数.
等量面 曲面f(x,y,z)=c(c为常数)为函数u=f(x,y,z)的等量面.
梯度与等量面的关系 函数u=f(x,y,z)在点P(x,y,z)的梯度的方向与过点P的等量面f(x,y,z)=c在这点的法线的一个方向相同,且从数值较低的等量面指向数值较高的等量面,而梯度的模等于函数在这个法线方向的方向导数.