三重积分的概念及其计算法
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第175页(1549字)
三重积分的定义 设f(x,y,z)在空间有界闭区域Ω上有界,将Ω任分为n个小闭区域△v(它也表示其体积)(i=1,2,…,n)在△v(i=1,2,…,n)上任取一点(ξ,ηi,ξi)做和式

如果当各闭区域直径中的最大值λ趋于零时,这和式的极限存在,则称此极限为函数f(x,y,z)的三重积分,记作 ,即
,即

此时也称f(x,y,z)在Ω上可积.其中f(x,y,z)称为被积函数,x,y,z称为积分变量,dv称为体积元素,Ω称为积分域.
三重积分的性质 与二重积分的性质类似.

三重积分在直角坐标系中的计算方法
体积元素:dv=dxdydz.

积分域作如下假定:作与z轴平行的直线除边界外,与闭区域Ω的边界曲面的交点不超过两点A,B.它们的z坐标分别为z1(x,y),z2(x,y)(z1(x,y)≤z2(x,y)),Ω在Oxy平面上的投影闭区间为D,则

内积分对z积分时,x,y视作常数.外积分为在闭区域D上二重积分,按二重积分在直角坐标系中的方法计算.
三重积分在柱坐标系中的计算方法
体积元素:dv=rdrdθdz.
三重积分:

Ω在平面Oxy上的投影域为D,则

其中z1(rcosθ,rsinθ),z2(rcosθ,rsinθ)是与平行z轴的直线交Ω边界曲面的两个z坐标(z1≤z2).
上式也可写为

三重积分在球坐标系中的计算方法 体积元素:dv=r2sinθdrdθdφ,r,θ,φ为球坐标,如图10.7所示.

图10.7
三重积分为

其中0≤r<+∞,0≤θ≤π,0≤φ≤2π.
下面分两种情况介绍.
(1)如果原点在Ω内,而Ω的边界曲面在球坐标系中的方程为r=r(θ,φ),则

(2)如果原点不在Ω内,且积分域Ω可表示为α≤φ≤β(α,β为常数),θ1(r)≤θ≤θ2(φ),r1(θ,φ)≤r≤r2(θ,φ),则
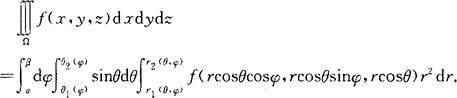
例如:积分域Ω:x2+y2+z2≤2Rz可以表示为

则
