曲线积分的定义、性质和计算

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第182页（2624字）

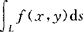对弧长曲线积分(或称第一型曲线积分)的定义 设L为()xy平面内的一条光滑曲线(逐段光滑曲线)，函数f(x，y)在L上有界，将L上任意插入n－1个分点，把L分成n个小段，记第i个小段的长度为△si，在第i个小段上任取一点(ξi，ηi)，作乘积f(ξi，ηi)△si(i=1，2，…，n)，并作和式i．如果当各小段的长度的最大值λ→0时，该和式的极限存在，则称此极限为函数f(x，y)在曲线弧L上对弧长(或第一型)的曲线积分，记作，即

其中f(x，y)称为被积函数，L称积分路径，f(x．y)ds称被积分式，ds称为弧微分．

上述定义可推广到空间曲线L的情形，即

弧长曲线积分的性质

弧长曲线积分的计算公式

(1)设f(x，y)在L上连续，函数x=φ(t)，y=ψ(t)在t∈［α，β］上有一阶连续导数，且φ′²(t)+ψ′²(t)≠0，则

(α≤β)且当t由α变到β时对应在L上的点，恰好画出曲线L．

(2)如果曲线L以y=y(x)或x=x(y)给出，则

或

其中a，b对应着曲线L的两个端点的横坐标或纵坐标．

(3)如果曲线L以极坐标形式给出，则

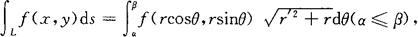
其中α，β对应着曲线L两个端点的幅角．

(4)如果空间曲线L的方程为

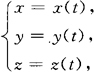
则

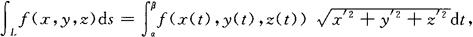
其中α，β对应着空间曲线L的两个端点(α≤β)．

对坐标(或第二型)曲线积分的定义 设L为Oxy平面内从点A到点B的一条有向光滑曲线．函数P(x，y)，Q(x，y)在L上有界．在沿L的方向上任意插入n－1个点M₁(x₁，y₂)，M₂(x₂，y₂)，…，M_n－1(x_n－1，y_n－1)，M0=A，M_n=B，令△x_i=x_i－x_i－₁，△y_i=y_i－y_i－1，在M_i－1M_i上任取一点(ξ_i，η_i)(i=1，2，…，n)，作和式，如果

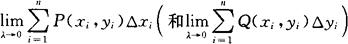
存在，则称此极限为函数P(x，y)(或Q(x，y))在有向曲线上的对坐标x(或对坐标y)的曲线积分，记作

即

类似地，可定义空间曲线L上的对坐标的曲线积分，即

对坐标曲线积分的性质

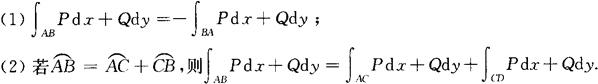
组合曲线积分的定义

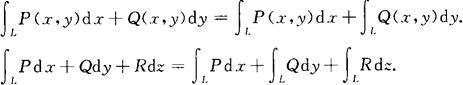
闭路积分记为

对坐标曲线积分的计算方法

(1)设P(x，y)，Q(x，y)在有向曲线L上连续．L的参数方程为x=φ(t)，y=ψ(t)，当参数t单调地由α变到β时，其对应在L上的点从起点A沿L运动到终点B．且φ(t)，ψ(t)有一阶连续导数，φ′²(t)+ψ′²(t)≠0，则

其中α不一定小于β．

(2)如果有向曲线L以y=y(x)形式给出，则

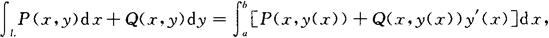
x=a对应着有向曲线L的起点，x=b对应着L的终点，a不一定小于b．当x由a变到b时，对应点恰好画出曲线L．

(3)如果有向曲线L以x=x(y)给出，则

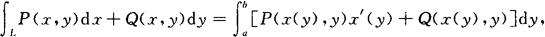
y=a对应着有向曲线L的起点，y=b对应着曲线的终点，a不一定小于b．当y由a变到b时，对应着的点恰好画出曲线L．

(4)如果有向曲线L以极坐标形式r=r(θ)给出，则

Q(rcosθ，rsinθ)(r′sinθ+rcosθ)］dθ．

θ=α对应着有向曲线L的起点，θ=β对应着L的终点，α不一定小于β．θ由α变到β时，对应着的点恰好画出曲线L．

(5)如果空间有向曲线L的方程为x=x(t)，y=y(t)，z=z(t)，则

t=α对应着有向曲线L的起点，t=β对应着L的终点．t=α变到t=β时，对应着的点恰好画出曲线L

两类曲线积分之间的关系

(1)平面曲线

其中α，β为有向曲线L上点(x，y)处的切线向量的方向角(见图11．1)．

图11．1

(2)空间曲线

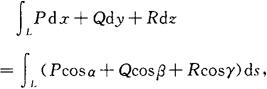
其中α，β，γ为有向曲线L上点(x，y，z)处的切线向量的方向角．