离散型随机变量的概率分布
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第377页(2826字)
分布律 P{X=xk}=pk,k=1,2,…

求X的分布律要特别注意两点:
(1)首先确定X的取值,通常是根据X的实际情况确定X的取值范围.
(2)求出X取各个值时的概率.X取某个值总是对应着某个随机事件,这个随机事件的概率就是随机变量取对应值的概率.
几个重要的离散型随机变量的概率分布
1.(0-1)分布

2.二项分布
(1)伯努利试验:设试验重复进行n次,若各次出现什么结果互不影响,则称这n次试验相互独立.若将试验E独立地重复进行n次,如果每次试验都只有两个结果A或 ,则称这个试验为n重伯努利试验.伯努利试验是一个很重要的数学模型.
,则称这个试验为n重伯努利试验.伯努利试验是一个很重要的数学模型.
(2)二项分布:在n重伯努利试验中,若P(A)=p, .记X为n次试验中事件A发生的次数,显然X是一个随机变量,它的取值为0,1,2,…,n,它的分布律为
.记X为n次试验中事件A发生的次数,显然X是一个随机变量,它的取值为0,1,2,…,n,它的分布律为 ,k=0,1,2,…,n,
,k=0,1,2,…,n,
称X服从参数为n,p的二项分布,记为X~B(n,p).
二项分布是一种非常重要的分布,在实践中大量存在,有着广泛的应用,特别是在产品的抽样检查中用得最多.
(3)二项分布与(0-1)分布有着密切关系:
其一,在二项分布中,若n=1,二项分布就变成(0-1)分布;
其二,在n次伯努利试验中,若只考虑某一次试验,比如第i次试验,可定义随机变量Xi如下:

Xi服从(0-1)分布.对前面的X,显然有 .而X服从二项分布.所以说:n个服从(0-1)分布的且相互独立的随机变量Xi的和服从二项分布.
.而X服从二项分布.所以说:n个服从(0-1)分布的且相互独立的随机变量Xi的和服从二项分布.
(4)二项分布分布律中概率的最大值问题:X~B(n,p).
①取k0=[(n+1)p],P{X=k0}为分布律中的最大值;[·]为取整记号.
②若(n+1)p=k0为整数,则P{X=k0}=P{X=k0-1}同为分布律中的最大值.
3.泊松分布
(1)定义:对于常数λ>0,如果随机变量X的分布律为

则称X服从参数为λ的泊松分布,记为X~P(λ).
(2)泊松定理:设有X~B(n,pn)和常数λ>0,如果npn=λ,则

泊松定理说明,当n→+∞时,二项分布的极限分布为泊松分布.这从理论上说明了泊松分布的来源.另一方面也表明,当n很大很大时,二项分布可以用泊松分布近似代替.
实践中,对X~B(n,p)的情况,当n≥50,np≤10时,记λ=np.则有

(3)泊松分布分布律中概率的最大值问题
①取k0=[λ],P{X=k0}是分布律中的最大值;
②若λ为整数,P{X=λ}=P{X=λ-1}同为最大值.
4.超几何分布
模型实例:设有产品l件,其中正品N件,次品M件(l=M+N),从中随机地抽取n件,n≤min(N,M),记X为其中的正品件数,求X的分布律.
X取值为0,1,2,…,n.
(1)有放回抽取:记 ,
, ,看成n重伯努利试验.
,看成n重伯努利试验.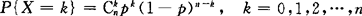 ,
,
X~B(n,p),即参数为n,p的二项分布.
(2)不放回抽取:按古典概型处理

称X服从超几何分布.
当产品总数无限增多时,正品数、次品数都无限增多时,并记 ,
,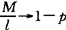 ,则有
,则有

说明超几何分布的极限分布为二项分布.
当产品总数很大时,或说n相对于l,M,N很小时,有

5.负二项分布(帕斯卡(Pascal)分布)
模型实例:在伯努利试验中,A表示“成功”, 表示“失败”.P(A)=p,
表示“失败”.P(A)=p, 1-p.引入随机变量X,它表示第r次成功出现在第X次试验.显然X取值为r,r+1,….求X的分布律P{X=k},k=r,r+1,….
1-p.引入随机变量X,它表示第r次成功出现在第X次试验.显然X取值为r,r+1,….求X的分布律P{X=k},k=r,r+1,….
这个问题可以这样描述:第r次成功正好出现在第k次试验.前k-1次试验中正好有r-1次成功.若记Y为前k-1次试验中成功的次数,显然Y~B(k-1,p),即 .第k次正好是成功,概率为p.所以P{X=k}=P{Y=r-1}·p,即
.第k次正好是成功,概率为p.所以P{X=k}=P{Y=r-1}·p,即

称X服从负二项分布.
6.几何分布
在负二项分布中,若r=1,分布律就成为
P{X=k}=p(1-p)k-1,k=1,2,….
这时称X服从几何分布.
几何分布是负二项分布的特例.它描述了“首次(第一次)成功出现在第k次试验”的数学模型.