长期债券投资的核算
出处:按学科分类—经济 中国商业出版社《金融企业会计制度实施手册上》第366页(14780字)
(1)长期债券投资是指公司购入的1年(含1年)内不能变现或不准备变现的债券,或者说是不准备随时变现、预计持有时间超过1年的债券投资。
(2)投资成本、利息、溢折价等等间的关系
实际支付价款-到期未领利息=投资成本,
投资成本-未到期利息-相关费用=投资时的账面值,
投资时账面值-面值=溢价(差额>0)或折价(差额<0),
面值+溢价=投资时账面值(溢价发行的债券),
面值-折价=投资时账面值(折价发行的债券)。
例如,某银行1998年1月1日发行3年期债券,面值1000元,票面年单利率12%,债券期满一次还本付息。某保险公司1999年3月1日购入10张这种债券,支付价款为12800元,其中包含尚未领取的1998年利息1200元,也包含相关税金、手续费400元。保险公司购入这批债券持到期满。
可见保险公司购入这批债券是作为长期投资。实际支付的价款中包含债券面值10000元,相关费用400元,到期未领利息10000×12%×1=1200元,未到期利息10000×12%×2÷12=200元。所以有:投资成本=12000-1200=10800元,投资时账面值=10800-400-200=10200元,溢价=10200-10000=200元。
(3)为核算长期债券投资,公司设置“长期债券投资”账户,下设四个明细科目:
①面值;
②相关费用,是指购买债券发生的税金、手续费等;
③应计利息,是指长期债券投资的未到期利息;
④溢折价。
长期债券投资应按期计算利息,并记入“长期债券投资-应计利息”账户;对于到期未领利息,再从“长期债券投资-应计利息”账户转入“应收利息”账户。
溢折价,从债券购入到期满在确认债券利息收入时用直线法或实际利率法摊销。
税金、手续费等通过“长期债券投资-相关费用”科目核算,从债券购入到期满在确认债券利息收入时分次摊销,计入投资收益;若相关费用数额不大,则可在取得时一次摊销,直接计入当期投资收益。
(4)会计分录。
①进行长期债券投资时,
借:长期债券投资-面值
-溢折价(若溢价)
-相关费用(若相关费用数额较大)
投资收益(若相关费用数额不大)
贷:银行存款(实际支付价款)
长期债券投资-溢折价(若折价)
②若长期债券投资实际支付价款中包含到期未领利息和未到期利息,则,
借:长期债券投资-面值
-溢折价(若溢价)
-应计利息(未到期利息)
-相关费用(若相关费用数额较大)
投资收益(若相关费用数额不大)
应收利息(到期未领利息)
贷:银行存款(实际支付价款)
长期债券投资-溢折价(若折价)
③溢价长期债券投资每期计算利息时,
借:长期债券投资-应计利息
贷:长期债券投资-溢折价(溢价分摊)
长期债券投资-相关费用(相关费用分摊)
投资收益
保险保障基金(以保险保障基金投资长期债券产生的收益)
保费收入(以保户储金投资长期债券产生的收益按约
定转入保费收入的部分)
④折价长期债券投资每期计算利息时,
借:长期债券投资-应计利息
-溢折价(折价分摊)
贷:长期债券投资-相关费用(相关费用分摊)
投资收益
保险保障基金(以保险保障基金投资长期债券产生的收益)
保费收入(以保户储金投资长期债券产生的收益按约
定转入保费收入的部分)
⑤出售长期债券投资时,
借:银行存款(实际收到金额)
长期债券投资-溢折价(尚未摊销的折价)
投资收益(若为损失)
保险保障基金
贷:长期债券投资-面值
-相关费用(尚未摊销的相关费用)
-溢折价(尚未摊销的溢价)
-应计利息(已计未到期利息)
应收利息(已计到期未领利息)
投资收益(若为收益)
保险保障基金
保费收入
⑥长期债券投资期满收回本息时,
借:银行存款(实际收到金额)
长期债券投资-溢折价(最后一期折价摊销)
投资收益(若为损失)
保险保障基金
贷:长期债券投资-面值
-相关费用(最后一期相关费用摊销)
-溢折价(最后一期溢价摊销)
-应计利息(已计未到期利息)
应收利息(已计到期未领利息)
投资收益(若为收益)
保险保障基金
保费收入
(5)注意区分:
①长期债券投资的一次付息与分次付息;
②溢价与折价;
③相关费用金额大与小;
④到期未领利息与未到期利息;
⑤溢折价摊销的直线法与实际利率法;
⑥计算实际利率用终值相等还是现值相等;
⑦实际利率法摊销溢折价用摊销表还是代数方法;
⑧发行日或付息日购买的债券与相邻两付息日之间购买的债券。
例.某银行1995年1月1日发行五年期债券,票面年单利率12%,面值1000元。债券期满一次还本付息。某保险公司于债券发行当天按1050元的价格购入80张作为长期投资,另支付有关税费400元。假设保险公司按年计算利息,那么计算利息并分别按直线法和实际利率法摊销溢价的会计处理如下:
(1)购入债券时,
投资成本=80×1050+400=84400元,
投资时账面值=84400-400=84000元
债券面值=80×1000=80000元,
债券溢价=84000-80000=4000元。
会计分录为,
借:长期债券投资-面值 80000
-溢折价 4000
投资收益 400
贷:银行存款 84400
(2)每年底计算利息并按直线法摊销溢价,
每年利息=80000×12%=9600元,
直线法摊销溢价,每年摊销额=4000÷5=800元,
会计分录如下(每年相同),
借:长期债券投资-应计利息 9600
贷:长期债券投资-溢折价 800
投资收益 8800
(3)每年底计算利息并按实际利率法摊销溢价,
①计算实际年利率i:设债券期限的年数为n,本题中n=5,由终值相等:
投资时账面值(1+i)5=债券期满收回的本利和
得:84000(1+i)5=80000(1+12%×5)
i=8.78929%
②通过溢折价摊销表计算溢折价摊销额
计算复利实际年利率条件下每年应收利息r,
由 ,
,
其中

得
r=8054(元)
债券溢折价各年摊销额见表3-2-1。
表3-2-1 债券溢折价摊销表

其中,“应收利息”是债券面值每年应取得的均等收益;“利息收入”是投资账面值实际取得的收益。
③计算各年溢折价摊销额的代数方法。
设xk表示第k年溢价摊销额(k=1,2,3,4,5),则各年溢折价摊销额之和等于溢折价总额,考虑时间价值后各年溢折价摊销额应该相等,即有下列方程组:

化简得
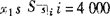
代入
1+i=1.0878929
解得
x1=671,x2=730,x3=794,x4=864,x5=941。
可见,代数方法与摊销表方法计算的结果相同。
④会计分录如下:
A.1995年12月31日,
借:长期债券投资-应计利息 9600
贷:长期债券投资-溢折价 671
投资收益 8929
B.1996年12月31日,
借:长期债券投资-应计利息 9600
贷:长期债券投资-溢折价 730
投资收益 8870
C.1997年12月31日,
借:长期债券投资-应计利息 9600
贷:长期债券投资-溢折价 794
投资收益 8806
D.1998年12月31日,
借:长期债券投资-应计利息 9600
贷:长期债券投资-溢折价 864
投资收益 8736
E.1999年12月31日。
借:长期债券投资-应计利息 9600
贷:长期债券投资-溢折价 941
投资收益 8659
(4)债券期满收回本金和利息,
借:银行贷款 128000
贷:长期债券投资-面值 80000
-应计利息 48000
例:某银行1995年1月1日发行五年期债券,票面年单利率12%,债券面值000元。该债券每年付息一次,最后一年还本金并付最后一次利息。某保险公司于债券发行当天按每张1050元的价格购入80张作为长期投资,另支付有关税费400元。假设保险公司按年计算利息,那么计算利息并分别按直线法和实际利率法摊销溢价的会计处理如下:
(1)购入债券时,
投资成本80×1050+400=84400,
投资时账面值84400-400=84000元,
债券面值80×1000=80000,
债券溢价84000-80000=4000。
会计分录为,
借:长期债券投资-面值 80000
-溢折价 4000
投资收益 400
贷:银行存款 84400
(2)每年底计算利息并按直线法摊销溢价
每年利息=80000×12%=9600元,
直线法摊销溢价,每年摊销额=4000÷5=800元,
会计分录如下(每年相同),
借:应收利息 9600
贷:长期债券投资-溢折价 800
投资收益 8800
(3)每年底计算利息并按实际利率法摊销溢价
①计算实际年利率i:设债券期限的年数为n,本题中n=5,由终值相等:
投资账面值(1+i)n
=债券期满收回本金+各期收取债券利息的终值
得:
化简为: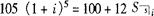
令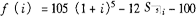
根据线性插值法求i。反复试验后,得



②用债券溢折价摊销表计算各年溢折价摊销额
设复利实际年利率条件下每年末应收利息为r,则
 #
#
r=9600(元)
债券溢折价各年摊销额见表3-2-2。
表3-2-2 债券溢折价摊销表

其中:8648,按公式计算应为8625。相差23元是实际利率精确度以及运算中四舍五入造成的。为使溢价正好摊销完,最后一年必须调整,实际利息多收入23元。
③计算各年溢折价摊销额的代数方法
设Xk表示第k年溢折价推销额(k=1,2,3,4,5),则各年溢折价摊销额之和等于溢折价总额,考虑时间价值后各年溢折价摊销额应该相等,即有方程组:
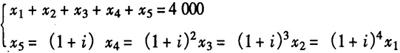
化简得

代入
1+i=1.106542
解得
x1=647,x2=716,x3=792,x4=876,x5=970。
可见,本题中代数方法与摊销表方法的计算结果略有出入,原因在于实际利率的精确度以及运算中的四舍五入。
④会计分录如下(按摊销表计算结果):
A.1995年12月31日,
借:应收利息 9600
贷:长期债券投资-溢折价 650
投资收益 8950
B.1996年12月31日,
借:应收利息 9600
贷:长期债券投资-溢折价 720
投资收益 8880
C.1997年12月31日,
借:应收利息 9600
贷:长期债券投资-溢折价 796
投资收益 8804
D.1998年12月31日,
借:应收利息 9600
贷:长期债券投资-溢折价 881
投资收益 8719
E.1999年12月31日,
借:应收利息 9600
贷:长期债券投资-溢折价 952
投资收益 8648
(4)各年收到债券利息(最后一年除外),
借:银行存款 9600
贷:应收利息 9600
(5)债券期满收回本金和最后一年利息,
借:银行存款 89600
贷:长期债券投资-面值 80000
应收利息 9600
注:①会计核算的精确程度是相对而言的,并非绝对精确。以上两例中,实际利率的计算、实际利率法最后一期摊销溢折价、直线法摊销溢折价、小额相关费用摊销、溢折价的摊销期(年、季、月)选择等等都存在近似取值。原因在于要权衡会计精确程度与财务费用。
②实际利率的精确值可通过叠代运算求得,但繁锁。
例.某银行1996年1月1日发行3年期债券,面值1000元,票面年单利率8%,到期一次还本付息。某保险公司于发行当日按每张债券950元的价格购入80张作为长期投资,另支付有关税费300元。假设保险公司按年计算利息,用实际利率法摊销折价,以代数法计算各年折价摊销额(精确到元)。列必要算式并做每笔业务的会计分录。
(1)购入债券时,
投资成本80×950+300=76300元,
投资时账面值76300-300=76000元,
债券面值80×1000=80000元,
债券折价76000-80000=-4000元。
会计分录为,
借:长期债券投资-面值 80000
投资收益 300
贷:银行存款 76300
长期债券投资-溢折价 4000
(2)按实际利率法摊销折价,
①计算实际年利率i:设债券期限的年数为n,本题中n=3,由终值相等:
投资时账面值(1+i)3=债券期满收回的本利和
得:
76000(1+i)3=80000(1+8%×3)
i=9.3%
②用代数方法计算各年溢折价的摊销额
设xk表示第k年溢折价摊销额(k=1,2,3),则各年溢折价摊销额之和等于溢折价总额,考虑时间价值后各年溢折价摊销额应该相等,即有方程组:
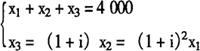
化简得

代入
1+i=1.093
解得
x1=1217,x2=1330,x3=1454。
(3)每年底计算利息并摊销折价
每年利息=80000×8%=6400元,
会计分录如下:
A.1996年12月31日,
借:长期债券投资-应计利息 6400
-溢折价 1217
贷:投资收益 7617
B.1997年12月31日,
借:长期债券投资-应计利息 6400
-溢折价 1330
贷:投资收益 7730
C.1998年12月31日,
借:长期债券投资-应计利息 6400
-溢折价 1454
贷:投资收益 7854
(4)债券期满收回本息,
借:银行存款 99200
贷:长期债券投资-面值 80000
-应计利息 19200
例:某银行1996年1月1日发行3年期债券,票面年单利率10%,到期一次还本付息。某保险公司于1996年3月15日以2060000元的价格购入面值为2000000元的债券作为长期投资。假设保险公司按年计算利息,用实际利率法摊销溢折价,以代数法计算各年溢折价摊销额(精确到元),列必要算式并做每笔业务的会计分录。
解:该题中,购买债券的行为发生在债券发行日与付息日之间,可归类到相邻两付息日之间购买的债券。买价中包含了未到期利息,在计算实际利率时需要注意这一特殊性。
(1)1996年3月15日购买债券时,
投资成本=2060000元。
未到期利息=2000000×10%×2.5÷12=41667元,
投资时账面值=2060000-41667=2018333元,
溢价=2018333-2000000=18333元。
借:长期债券投资-面值 2000000
-应计利息 41667
-溢折价 18333
贷:银行存款 2060000
(2)计算实际年利率
设债券投资的实际利率为i,
投资年数为n=(12-2.5)÷12+2=2.791667年,
由终值相等:
投资时账面值(1+i)n=债券期满收回的本利和
得:
2018333(1+i)2.791667=2000000(1+10%×3)
解得 i=0.09495
(3)计算各年溢折价摊销额
设xk表示第k年溢折价摊销额(k=1,2,3),则各年溢折价摊销额之和等于溢折价值总额,考虑时间价值后各年溢折价摊销额应该相等,即有方程组:

化简得
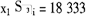
代入
1+i=1.09495
解得
x1=5566,x2=6094,x3=6673
(4)每年底计算利息并摊销溢折价的会计分录
A.1996年末,
当年利息=2000000×10%×9.5÷12=158333元,
借:长期债券投资-应计利息 158333
贷:长期债券投资-溢折价 5566
投资收益 152767
B.1997年末,当年利息=2000000×10%=200000元,
借:长期债券投资-应计利息 200000
贷:长期债券投资-溢折价 6094
投资收益 193906
C.1998年末,当年利息=2000000×10%=200000元,
借:长期债券投资-应计利息 200000
贷:长期债券投资-溢折价 6673
投资收益 193327
(4)债券期满收回本息,
借:银行存款 2600000
贷:长期债券投资-面值 2000000
-应计利息 600000
本节涉及到年金的计算和债券的计算,详见以下两节。