点的复合运动
书籍:现代综合机械设计手册上
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第70页(998字)
2.3.1 绝对运动、相对运动和牵连运动
绝对运动:研究对象相对于定参考系(通常视地面参考系为定系)的运动称为绝对运动。点在绝对运动中的速度、加速度称为绝对速度和绝对加速度,用 ,
,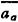 表示。
表示。
相对运动:研究对象相对于动参考系的运动称为相对运动。点在相对运动中的速度、加速度称为相对速度和相对加速度,用 ,
, 表示。
表示。
牵连运动:动参考系相对于定参考系的运动称为牵连运动。动参考系在牵连运动中,其上与动点重合之点的运动速度、加速度称为动点在此瞬时的牵连速度和牵连加速度,用 和
和 表示。
表示。
2.3.2 运动的分解与合成
研究对象的任一绝对运动,总可分解为它相对于某一确定动系的相对运动和随同该动系的牵连运动;反之研究对象相对于某一动系的相对运动和它随同该动系的牵连运动总可合成为研究对象相对于定系的唯一的绝对运动。因此,绝对运动也称为相对运动和牵连运动的复合运动。总之,复合运动的概念是指:

2.3.3 点的科氏(科里奥利)加速度
在研究点的复合运动时,由于动系的转动角速度 。和点的相对速度
。和点的相对速度 、共同影响,使动点在绝对运动中所具有的加速度称为科氏加速度,用
、共同影响,使动点在绝对运动中所具有的加速度称为科氏加速度,用 表示.它的矢量表达式为
表示.它的矢量表达式为

2.3.4 点的速度、加速度合成定理
见表1.2-11。
表1.2-11 点的速度,加速度合成定理

2.3.5 点的速度、加速度合成定理应用实例
见表1.2-12。
表1.2-12 点的速度、加速度合成定理应用实例


上一篇:刚体的基本运动
下一篇:现代综合机械设计手册上目录