格论
书籍:自然辩证法辞典
更新时间:2018-11-17 05:40:17
出处:按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第688页(535字)
是近世代数学的一个分支。
指一类很重要的代数系统。大约形成于1935年左右。
设A是一个集合,如果A上的一个关系≤,满足自反性,反对称性和传递性,则称≤是A上的偏序关系,二元组<A,≤>称为偏序集。设T是偏序集(A,≤)的子集,如果x∈T,x≤b(b≤x),则A的元素b说是T的一个上(下)界。
T的上(下)界中最小(大)者,称为T的最小(大)上(下)界。对于一个偏序集(A,≤),如果A中任意两个元素都有最小上界和最大下界,则称<A,≤>为偏序格。
格还可以有另外一种定义,即代数格,可以证明,偏序格和代数格是等价的,即给定一个偏序格可以诱导与之等价的代数格,反之,给定一个代数格可以构造一个偏序格与之等价。由格的定义可知,格满足对偶原理,这对格的研究带来了很大方便。
格论是很有其实际背景的,例如:在计算机科学中被广泛应用的布尔代数,就是一种特殊的格。许多问题可以用格这个代数系统来描述,例如设集合S的幂集为ρ(S),关系≤为包含关系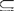 ,则(P(S),
,则(P(S),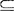 )为一偏序格。
)为一偏序格。
又如,设A是命题逻辑中所有命题的集合,≤是蕴含关系,则(A,≤)为一偏序格。正是基于此,格论已经引起了计算机科学工作者的重视,并在计算机科学中已经有了大量的应用。