方差分析法

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第368页（2026字）

极差分析法没有考虑试验误差的影响。在处理试验数据时，如果需要把因素水平变动引起的数据波动同试验误差引起的数据波动加以区别，就可以采用方差分析法。

仍以柱塞组合件收口强度稳定性试验为例，介绍方差分析法的基本内容。

对柱塞头高度B取2个水平(B₁=11．8毫米，B₂=11．9毫米)做单因素对比试验。试验数据如表4．4．6－1所示。

表4．4．6－1 柱塞组合件两个水平、单因素对比实验数据表

表中，“y_ij”表示第i个试验条件下重复第j次的试验数据。”

1．计算误差变动平方和

由于存在试验误差，使得B_i或B₂条件下的S次相同试验的5个数据各不相同。为了从总体上估计试验误差对数据变化的影响，需要求出各次试验误差的平方和，用它来描述试验误差引起的数据波动。这个试验误差的平方和就是所谓误差变动平方和，简称为误差变动，以S_误表示。计算S_误的公式是：

式中，m为水平数，k为各水平的试验次数。代入试验数据，得：S_误=6．2。

2．计算因素变动平方和

由表4．4－5可见，B₁和B₂水平的2个平均值5．6和7大致是围绕数据总平均值T=6．3波动的。所以，同前面估计试验误差的情况类似，可以用各水平下数据平均值与总平均值之差的平方和来估计因素水平变化引起的数据波动。这个平方和就是所谓因素变动平方和，简称为因素变动，以S_因表示。S_因的计算公式是：

代入本例试验数据，得到S_因=4．9

3．计算总的变动平方和

试验数据总的波动用全部数据y_ij与总平均值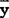之差的平方和来描述，这个平方和叫做总的变动平方和，简称为总的波动，用S_总表示。S_总的计算公式为：

一般情况下，S_总=S_误+S_因。

代入本例试验数据，得到S_总=11．1

4．计算平均变动平方和

为了分析因素水平变化对指标影响是否显着，需要把因素变动同误差变动进行比较。但是不能直接比较，因为S_因和S_误的大小均与试验数据的个数多少有关。必须在S_因和S_误分别除以各自的自由度(所谓自由度就是独立的数据个数)去消除数据个数多少的影响，然后才能进行比较。S_因、S_误、S_总的自由度分别以f_因、f_误、f_总表示，其计算公式为：

f_因=水平数－1 (4)

f_总=数据的总个数－1 (5)

f_误=f_总－f_因 (6)

有了自由度，就可以求出平均变动平方和(简称平均变动)。因素的平均变动为S_因／f_误，误差的平均变动为S_误／f_误。代入本例数据，得到S_误／f_因=4．9，S_误／f_误=0．775。

5．进行因素显着性检验

检验的步骤是：

(1)计算S_因／f_因，与S_误／f_误的比值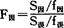。代入本例数据，得到F_B=6．32。

(2)查F分布表。F分布表列出了各种自由度下F的临界值F_αoF_α的下标α叫做信度，表示判断错误的概率。常用的F分布表有α=0．25，α=0．10，α=0．05，α=0．01等几种。一般认为若F_因＞F_0．05，则认为因素的影响是显着的；若F_因＞F_0．01，则因素的影响是高度显着的。本例查表得：

F_0．05(1，8)=5．32

F_0．01(1，8)=11．3

(3)比较F_B与F_αoF_B＞F_0．05，因素B是显着的。但由于F_B＞F_0．01，故B的影响不是高度显着的。

对于多因素试验，通常按一定程序在正交设计表上进行，应用起来也十分方便。