普通计数法

出处：按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第435页（2304字）

1．基本原理

如图8．5－1所示

图8．5－1 计数法测频

被测信号经放大整形后变成脉冲信号。内部晶振经分频后产生几种闸门信号。闸门信号打开电子门后，被测信号通过电子门进入计数条开始计数，闸门信号关闭电子门后，计数停止，并显示所计的数值。设闸门时间为τ，计的数值为N，则有：

或相对频率偏差

2．测量不确定度

对(8．5－2)式进行微分，即得y(τ)的测量不确定度。

设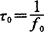为晶振的周期。

τ=nτ₀为闸门时间

则

由于频率实际值与标称值偏差都很小，故此式中可近似的取N≈f₀τ

则有

右边第二项为内部晶振周期的不确定度，它也等于晶振频率的不确定度。如果测量目的是测定被测频率的准确度，则这项不确定度是指内部晶振的频率准确度；如测量目的是被测频率的稳定度、则此项相应的也为内部晶振的稳定度。

右边第一项的dN为计数不准引入的误差，通常取dN±1，则第一项就是所谓±1计数误差。下边详细分析这一误差的来源及含义。

参看图8．5－2

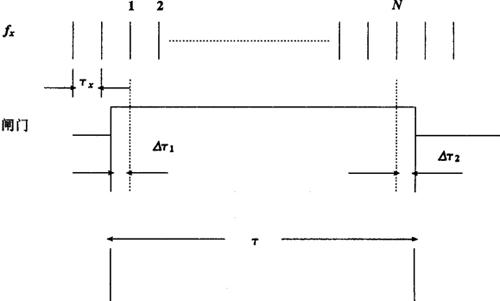
图8．5－2 ±1计数误差

设τ_x为被测信号的周期，从图中可得出严格的时间关系为：

τ=Δτ₁+(N－1)τ_x+Δτ₂

=Nτ_x+(Δτ₁+Δτ₂－τ_x) (8．5－4)

第二项是无法准确给出的测量误差，但可以求出每个误差的范围。

由图中看出0≤Δτ₁≤τ_x，0≤Δτ₂≤τ_x

故有－τ_x≤(Δτ₁+Δτ₂－τ_x)≤τ_x

相应的频率实际值应为

这意味着，实际频率比测得值N／τ可能高，但最高不会高出1／τHz；也可能低，但最低也不会低出1／τHz。故频率实际值可以写成

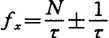
相应的(8．5－3)或可写成

第二项就是到±1引起的测量不确定度。

第一项为内部晶振的准确度或稳定度，可以人为的采用高稳晶振，甚至可以用原子频标代替，因而这一项可做到很小。但第二项是无法克服的，当f₀及τ一定时，此项就是计数法测频所能得到的最小不确定度，因而称为这种方法的测量分辨率。下边派生出的所有测量方法都是为了提高测量分辨率。

【参考文献】：

［1］王义遒等，量子频标原理，科学出版社，1986。

［2］吴守贤等，时间与频率，科学出版社，1983。

［3］黄秉英等，时间频率的精确测量，计量出版社，1986。

［4］王江现代测量技术，计量出版社，1987。

［5］P. Kartaschoff ,Frequency and Time,Academic Press ,1978.

［6］J. A. Barnes et al. ,Characterization of frequency stability, IEEE Trans Instrum Meas. IM —20,p.105—120,1971.

［7］Time and frequency:Theory and Fundamentals,NBS Manograph 140,1974.

［8］D. W. Allan ,The measurement of fruquency and frequency stability of precision oscillator,Proc.6th Ann PTTI Planning Meeting.

［9］Annual Report of the BIPM Time Sectina,1974.