物理光学中的一些基本定律

出处：按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第468页（5063字）

1．光程和光程差

光波在不同介质中的传播速度是不同的，把光波在某种介质中走过的几何距离l，折算成该光波在相同的时间内在真空中所走过的距离L，则L称为光波在这种介质中的光程。设光波在某种介质中的传播速度为v，则走过l所用的时间t=l／v，在这段时间里，该光波在真空中走过的路程等于L=c·t=c·l／v。根据折射率的定义，c／v是这种介质的折射率n，所以，光程等于介质的折射率乘光走过的几何距离，即：

L=nl (9．2－15)

在研究两束光通过不同介质时，需要分别计算这两束光的总光程，然后计算两束光的光程差δ，再由光程差计算它们的相位差：

2．光的干涉现象及其应用

干涉现象是波动过程的一个基本特征，只有波动的叠加才能产生干涉现象。只有频率相同、振动方向相同、相位相同或有固定相位差的两束光，才能产生干涉现象。平常所见到的漂浮在水面上的油膜或空中的肥皂泡所呈现的彩色条纹，就是光线产生干涉的结果，属于平行面薄膜的干涉现象。等厚薄膜上表面与下表面反射光的光程差δ由下式表示：

式中 e——薄膜厚度；

n——膜的折射率；

λ——入射光的波长；

r——折射角。

当光程差等于波长的整数倍时，振动加强，出现明条纹，当光程差等于半波长的奇数倍时，振动相抵消，出现暗条纹。如果规定光垂直入射到薄膜，则r=0°，cosr=1，上式可简化。从式中可以看到，如果选择适当的膜厚e和材料(适当的n值)可使某种波长的光在薄膜上获得高的反射或高的透射，用这种原理可制成干涉滤光片，它只让某个波长的光透过，而其他波长的光反射掉(必要时用带颜色的玻璃吸收掉一部分不需要的光)，从而可得到一束单色光。这种滤光片又称为窄带滤光片，通带半宽度约为3－10nm，峰值透射率约为30%－70%。

实际制造时，常采用多层镀膜的方法，以提高干涉滤光片的峰值透射率、降低通带宽度。

近年来，在光学工程上常使用一种冷光膜或冷光反射镜(聚光镜)，这种膜设计成让白炽光源所发出的大量红外线从后面透过去，而让有照明作用的可见光会聚到前方，既增加了被照面上的光照度，又不致于令被照面过份发热。

在复杂的光学镜头的每块透镜片上，按使用的光波波段，可设计出能大大减少镜片间的反射而增加透光本领的膜，称为增透膜，这种膜能大大改善镜头的成象质量。

3．光的衍射现象及其应用

衍射也称为绕射，当光通过小孔、狭缝或其他形状的孔隙时，并不完全按几何光学中所描述的沿直线行进，有很小部分的光能量可进入阴影之内，而且进入阴影内的光强分布是不均匀的，按一定规律强弱相间地排列，光的衍射现象是波动性的基本特征之一。

用衍射光栅来作为色散元件，是利用衍射现象的一个典型例子。图9．2－3是反射式刻划光栅的截面图，用作色散元件的光栅很密，每毫米有数百条刻线，多的可达每毫米2400条。

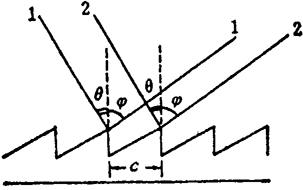
图9．2－3 反射式衍射光栅

由几何关系可以导出平面反射光栅的基本公式：

C(sinφ+sinθ)=±Kλ (9．2－18)

式中 C——光栅常数；

φ——衍射角；

θ——入射角；

K——为光谱级数。K=0，1，2，3……

λ——衍射光的波长

当K=0时，φ_b=－θ，表示零级光谱的衍射角与入射角相等，这时平面光栅相当于一块平面镜，而且在零级光谱中，不管波长等于多少，φ_b都是一样，没有色散作用。在近紫外至可见光谱区，一般都是用K=1时的一级光谱。

又从(9．2－18)式可以看到，对于K=1，2，3……等情况可有……也就是说对于某一入射角θ，波长等于λ的一级光谱的衍射角，与波长等于λ／2的二级光谱及波长等于λ／3的三级光谱的衍射角都是相同的，在同一个衍射角度上出现了多级光谱的重叠，例如在波长为700nm的一级光谱上会重叠着350nm的二级光谱。这种现象是光栅色散所特有的问题，所以，在光栅单色仪中，为了在一个衍射角度上获得唯一的一种波长的单色光，要采取一些消除级次重叠的措施。常用的方法是在光路中插入适当的前截止滤光片，它只允许大于某个波长的光通过，而把波长较短的高级次光谱截掉。

将式(9．2－18)对波长微分，可得光栅角色散的表达式：

可见光栅的角色散率与K成正比，与C成反比。为得到足够大的色散率，在可见光谱区一般采用每毫米600～1200条刻线的光栅。

光栅的理论分辨率与光栅的刻线总数N成正比，即

R=kN (9．2－20)

对于光栅常数一样的光栅来说，较大的光栅具有较高的分辨率。与棱镜色散元件相比，光栅比较容易达到较高的分辨率。且光谱中各谱线到中央条纹的距离也与波长成正比，可得到均匀排列的光谱。

4．光的偏振

光是电磁波，而电磁波已被证实是横波，表示电场强度的电矢量也叫光矢量，光矢量与传播方向所成的平面称为振动面。如果在传播过程中光矢量始终保持在一个固定的振动面内，这种光称为线偏振光，普通光源所发出的光，各个振动方向的振动都有，是杂乱无章的，从统计意义上讲各种方向的振动都一样多，这样的光称为自然光，如太阳光、普通灯光都属这一类。激光是一处特殊的光源，很多种激光具有固定的振动面，属于线偏振光。

有一些物质只能让某一个振动方向的光通过，而阻止其他振动方向的光。因而可以把自然光变成线偏振光，这种物质可以制成起偏器。某些天然晶体和某些长碳氢链结构的高分子透明材料可制成起偏器。现在用得比较普遍的是一种薄膜型的偏振片。

让偏振片表面垂直于光的传播方向，然后以光的传播方向为轴转动偏振片，如果发现通过偏振片后光的强弱有变化，则原入射光束是线偏振光或部分偏振光。

马吕斯定律指出，强度为I₀的偏振光，透过偏振片后，透射光的强度(不考虑吸收损失)为：

I=I₀cos²α (9．2－21)

式中，α为起偏器与检偏器两个偏振化方向的夹角。如果起偏器与检偏器的偏振化方向平行即α=0°或180°时，则I=I₀，光的强度最大，如果它们互成正交，即α=90°或270°时，I=0这时没有光从检偏器射出。一般情况下，起偏器和检偏器的质量不理想，即使正交时光强也不为零(约为入射光的0．1－0．01%)。如果考虑吸收、反射等损失，即使α=0°或180°，I也不会等于I₀，而只能达到某一最大值。

线偏振光通过某些物质时，其振动面会发生旋转，称为旋光现象。能使振动面旋转的物质称为旋光物质。石英晶体、松节油、各种糖类和某些医药，都有旋光性。旋光物质又分为左旋和右旋两类。如果面对入射光的方向观察，使振动面沿反时针方向旋转的物质称为左旋物质。反之，称为右旋物质。偏振面旋转的角度与入射光的波长有关，一般来讲，波长愈短旋光率愈大。对于一定波长的单色光，振动面旋转的角度与物质的厚度成正比。如果是溶液，旋转角度与浓度成正比：

φ=αcd (9．2－22)

式中 c——为浓度(g／cm³)；

d——光线通过的厚度(dm)；

α——为该液体的旋光率；

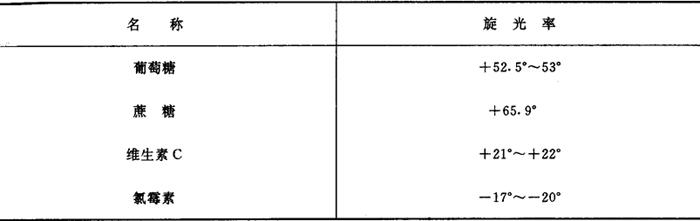
φ——为旋转角，单位为度。表9．2－2所示为一些物质在温度20℃时，对波长589．3nm单色光的旋光率，并以“+”表示右旋，“－”表示左旋。

表9．2－2 一些物质的旋光率

5．光的吸收和散射

光通过介质时，总会或多或少地被吸收，使入射光的强度减弱，其一般规律为：

I=I₀e^－k1 (9．2－23)

式中 I₀——为入射光的强度；

l——为光经过介质的距离；

k——为吸收系数，是波长的函数。

不同物质的K值相差很大，如光学玻璃K=10^－2～10^－4cm^－1，而有色玻璃K=3～6cm^－1。

对于溶液，吸收系数与溶液的浓度C成正比，即K=βC，β为与物质分子结构有关的系数，代入(9．2－23)式可得

I=I₀e^－βcl (9．2－24)

上式称为朗伯——比尔定律，在单色光和浓度不很大时能较好地与实验符合。

令，E=βlgC，则上式变为A=ECl，A称为吸收率(也叫光密度)，E称为消光系数。

当光线进入介质后，遇到悬浮的微小颗粒或不均匀的原子、分子团时，光线向四面八方散开，这种现象称为散射。散射光的多少与入射光的波长有关，也与介质中微粒的大小和多少有关，还与介质的温度有关。

散射光的波长与入射光波长相同的，称为瑞利散射。散射光的强度与光波频率的四次方成正比，称为瑞利定律。

散射光强度I与入射光强度I₀之间的关系可表示为：

I=I₀e^－hl (9．2－25)

式中l为光通过的距离，h为散射系数。

【参考文献】：

［1］现代计量学概论，鲁绍曾主编，中国计量出版社，1987。

［2］现代计量测试技术，王江主编，中国计量出版社，1990。

［3］光度学，郝允祥等编着，北京师范大学出版社，1988。

［4］色度学，荆其诚等编着，科学出版社1979，。

［5］Principles Governing Photometry，Metrologia，19，97－101，1983．

［6］Accurate Measurement and Correction for Nonlinearities in Radiometers，J．Res．NBS，67A，1972．